我们在线宽规则设置中提到过阻抗线的概念，那么什么是阻抗线呢？我们如何知道设计当中的信号走线线宽与间距呢？这个涉及阻抗计算。

10.3.1  阻抗计算的必要性

当电压、电流在传输线中传播时，特性阻抗不一致会造成所谓的信号反射现象等。在信号完整性领域里，反射、串扰、电源平面切割等问题都可以归为阻抗不连续问题，因此匹配的重要性在此展现出来。

10.3.2  常见的阻抗模型

一般利用Polar SI9000阻抗计算工具进行阻抗计算。在计算之前需要认识常见的阻抗模型。常见的阻抗模型有特性阻抗模型、差分阻抗模型、共面性阻抗模型。如图10-56所示阻抗模型又细分为如下几类。

（1）外层特性阻抗模型。

（2）内层特性阻抗模型。

（3）外层差分阻抗模型。

（4）内层差分阻抗模型。

（5）共面性阻抗模型。

① 外层共面特性阻抗模型。

② 内层共面特性阻抗模型。

③ 外层共面差分阻抗模型。

④ 内层共面差分阻抗.模型。

图10-56  常见的阻抗模型

10.3.3  阻抗计算详解

1．阻抗计算的必要条件

阻抗计算的必要条件有板厚、层数（信号层数、电源层数）、板材、表面工艺、阻抗值、阻抗公差、铜厚。

2．影响阻抗的因素

影响阻抗的因素有介质厚度、介电常数、铜厚、线宽、线距、阻焊厚度，如图10-57所示。

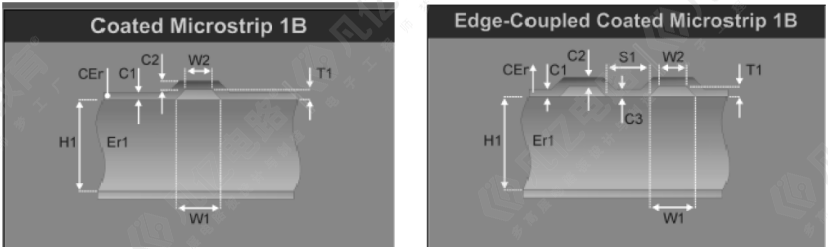
图10-57  影响阻抗的因素

在图10-57中，H1为介质的厚度（PP片或者板材，不包括铜厚）；Er1为PP片或者板材的介电常数，多种PP片或者板材压合一起时取平均值；W1为阻抗线下线宽；W2为阻抗线上线宽；T1为成品铜厚；CEr为绿油的介电常数（3.3）；C1为基材的绿油厚度（一般按照0.8mil）；C2为铜皮或者走线上的绿油厚度（一般按照0.5mil）。

一般来说，上、下线宽存在如表10-1所示的关系。

表10-1  上、下线宽关系表

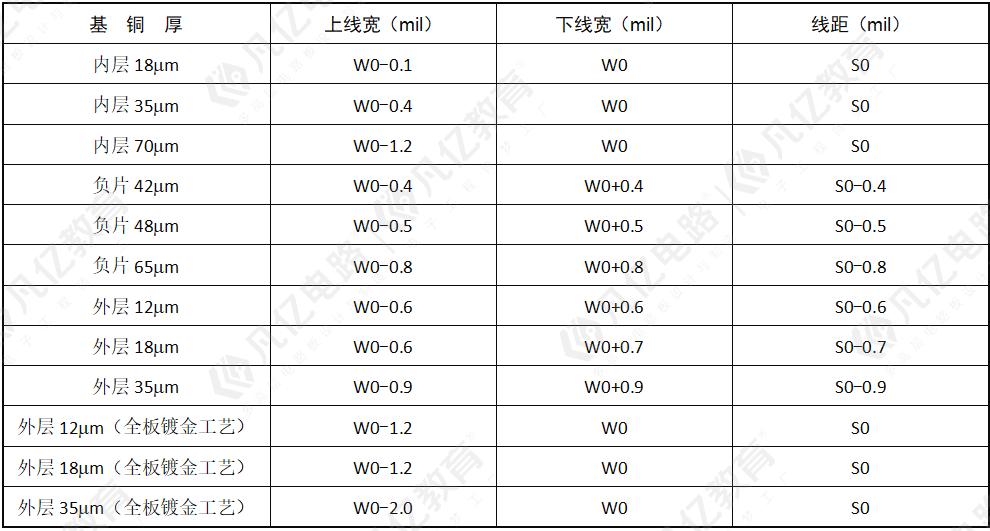
注：其中W0为设计线宽，S0为设计线距。

3．阻抗计算方法

下面通过一个实例来演示阻抗计算的方法及步骤。

普通的FR-4板材一般有生益、建滔、联茂等板材供应商。生益FR-4及同等材料芯板可以根据板厚来划分。表10-2列出了常见生益FR-4芯板厚度参数及介电常数。

表10-2  常见生益FR-4芯板厚度参数及介电常数

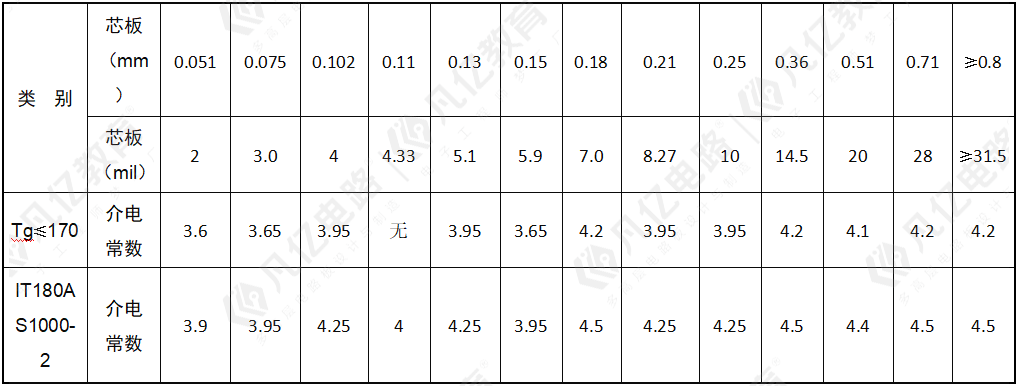
半固化片（即PP片）一般包括106、1080、2116、7628等。表10-3列出了常见PP片厚度参数及介电常数。

表10-3  常见PP片厚度参数及介电常数

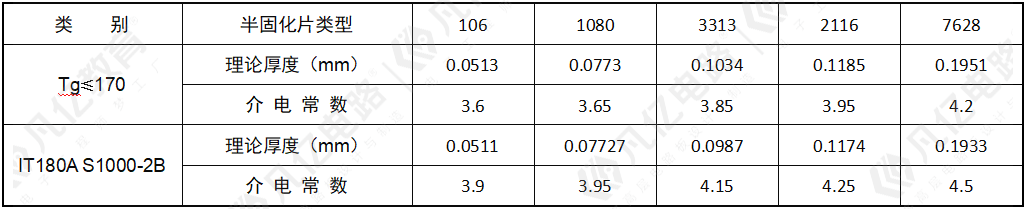
对于Rogers板材，Rogers4350 0.1mm板材介电常数为3.36，其他Rogers4350板材介电常数为3.48；Rogers4003板材介电常数为3.38；Rogers4403半固化片介电常数为3.17。

我们知道，每个多层板都是由芯板和半固化片通过压合而成的。当计算叠层结构时，通常需要把芯板和PP片叠在一起，组成板子的厚度。例如，一块芯板和两张PP片叠加“芯板+ 106+2116”，那么它的理论厚度就是0.25mm+0.0513mm+0.1185mm=0.4198mm。但需注意以下几点。

（1）一般不允许4张或4张以上PP片叠放在一起，因为压合时容易产生滑板现象。

（2）7628的PP片一般不允许放在外层，因为7628表面比较粗糙，会影响板子的外观。

（3）另外，3张1080也不允许放在外层，因为压合时也容易产生滑板现象。

（4）芯板一般选择大于0.11mm的，六层的一般两块芯板，8层的一般3块芯板。

由于铜厚的原因，理论厚度和实测厚度有一定的差额，具体可以参考图10-58。

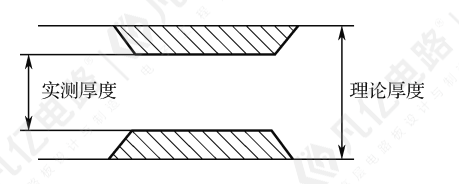
图10-58理论厚度与实测厚度

从图10-58中可以看出，理论厚度和实测厚度存在铜厚的差额，可以总结出如下公式。

实测厚度=理论厚度-铜厚1(1-X1)-铜厚2(1-X2)

式中，X1、X2表示残铜率，表层取1，光板取0。电源地平面残铜率一般取值为70%，信号层残铜率一般取值为23%。

残铜率是指板平面上有铜的面积和整板面积之比。例如，没有加工的原材料残铜率就是100%，蚀刻成光板时就是0%。

“OZ”表示铜厚单位“盎司”，1OZ=0.035mm。

10.3.4  阻抗计算实例

（1）叠层要求：板厚为1.2mm，板材为FR-4，层数为6层，内层铜厚为1OZ，表层铜厚为0.5OZ。

（2）根据芯板和PP片常见厚度参数组合，并根据叠层厚度要求，可以堆叠出如图10-59所示的叠层结构。

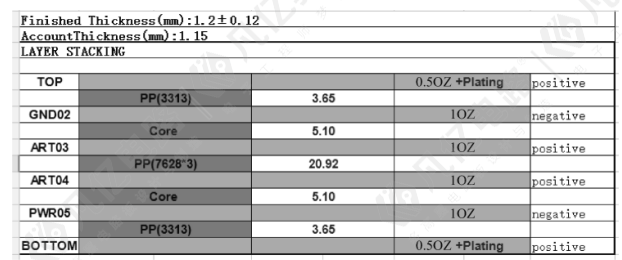
图10-59  6层叠层结构图

图10-58中标出的PP片厚度为实际厚度，计算公式如下。

PP（3313）[实测值]=0.1034mm[理论值]-0.035／2mm×（1-1）[表层铜厚为0.5OZ，残铜率取1]-0.035mm×（1-0.7）[内层铜厚为1OZ，残铜率取70%]=0.0929mm=3.65mil

PP（7628×3）[实测值]=0.1951mm×3[理论值]-0.035mm×（1-0.23）[内层铜厚为1OZ，相邻信号层残铜率取0.23%]-0.035mm×（1-0.23）[内层铜厚为1OZ，相邻信号层残铜率取0.23%]=0.5314mm=20.92mil

板子总厚度=0.5OZ+3.65mm+1OZ+5.1mm+1OZ+20.92mm+1OZ+5.1mm+1OZ+3.65mm+0.5OZ= 1.15mm

（3）打开Polar SI9000软件，选择需要计算阻抗的阻抗模型，计算表层50欧姆单线阻抗线宽。如图10-60所示，根据压合叠层数据，填入相关已知参数，计算得出走线线宽W0=6.8mil。这个是计算出比较粗的走线，有时候会基于走线难度准许阻抗存在一定的误差，所以可以根据计算得出的走线线宽来稍微调整。例如，调整计算参数走线线宽5.5mil时，计算阻抗Zo=54.82，如图10-61所示。

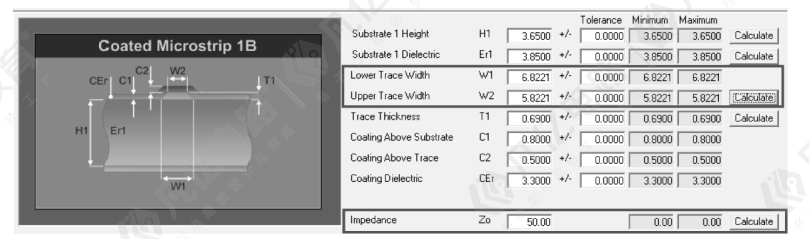
图10-60根据阻抗计算线宽

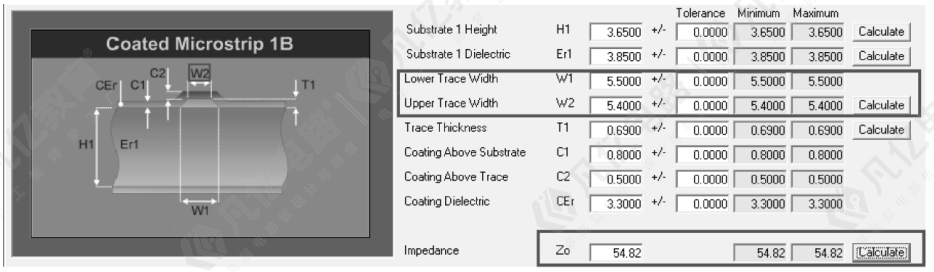
图10-61  根据线宽微调阻抗值

（4）需计算内层（以第3层为例）90欧姆差分阻抗走线线宽与间距，如图10-62所示，选择内层差分阻抗模型，根据压合叠层数据，填入已知参数，然后可以通过阻抗要求，调整线宽和间距，分别计算，考虑到板卡设计难度可以微调阻抗在准许范围之内即可。

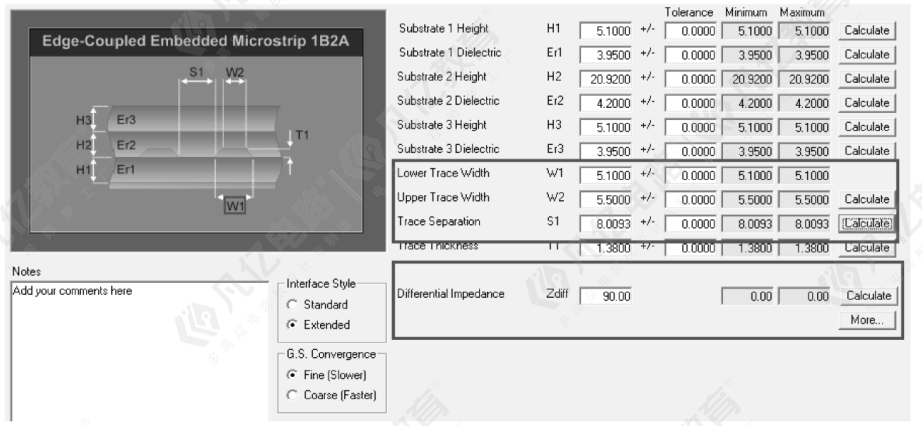
图10-62  90欧姆差分阻抗计算结果

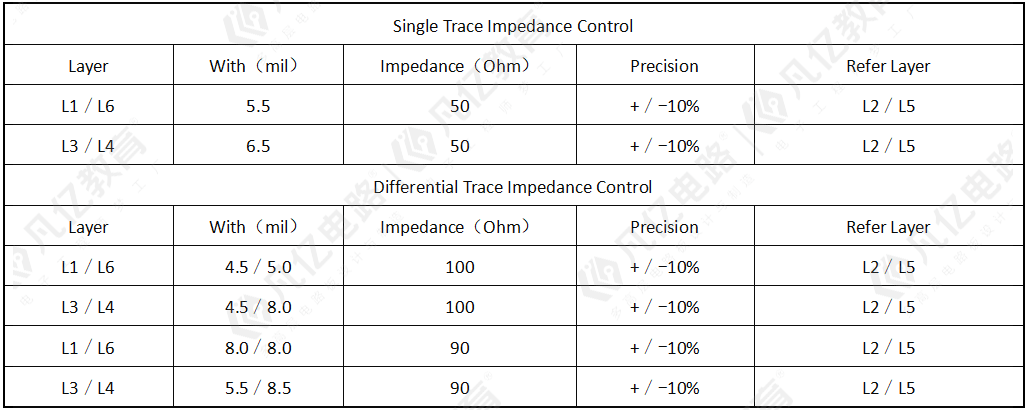
（5）最终计算结果如表10-4所示。

表10-4  阻抗计算结果