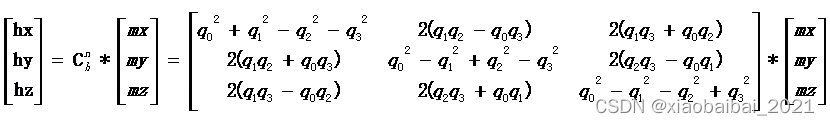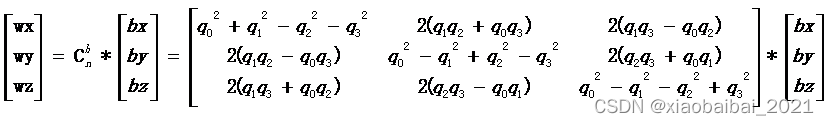大家好,我是学电子的小白白。本篇文章我们来讲讲如何将陀螺仪和加速度计的数据结合起来,获取更准确的姿态数据,使用的是互补滤波的方法。
阅读本文需有一定的知识基础,可以参见作者以前MPU6050的两篇文章:《MPU6050陀螺仪和加速度计数据的获取和校准》、《MPU6050官方DMP的移植和使用》,以及了解四元数的一些基本概念。
1)为什么要进行姿态融合在之前的文章里,我们讲过一些陀螺仪和加速度计的知识,我们知道,陀螺仪可以获取载体的角速度,由角速度积分,就能得到角度,也就得到了载体的姿态。但是,陀螺仪给出的角速度存在测量误差、噪声和漂移,经过积分运算之后,会形成累积误差,这个误差会随着时间延长越来越大,最终导致偏差太大而无法使用。
另一方面,加速度计可以测量到地球的重力,当载体静止或者匀速运动时,重力的方向就是竖直向下的,通过测量重力加速度的方向,可以获取当前载体的俯仰角、滚转角。但是加速度计容易受到高频噪声的干扰,动态响应慢,只在长时间内数据比较有效。
因此,一般我们使用加速度计的数据来修正陀螺仪,以加速度计获取的实时姿态角来修正陀螺仪的累积误差,就能在短时间和长时间内都能获取比较满意的姿态信息。
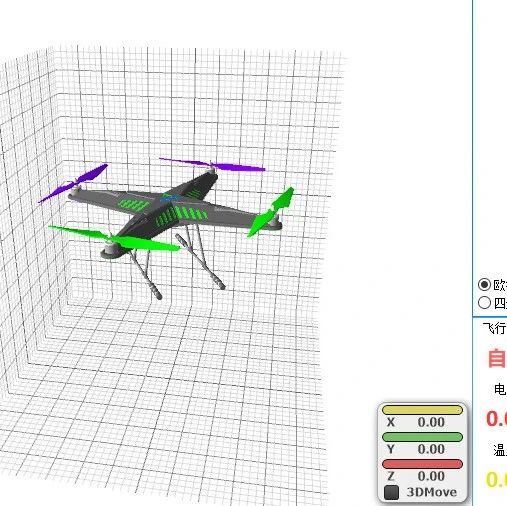
我们以下图为例,Z轴向上,约定绕X轴旋转的角度为滚转角;绕Y轴旋转的角度为俯仰角,绕Z轴旋转的角度为偏航角。
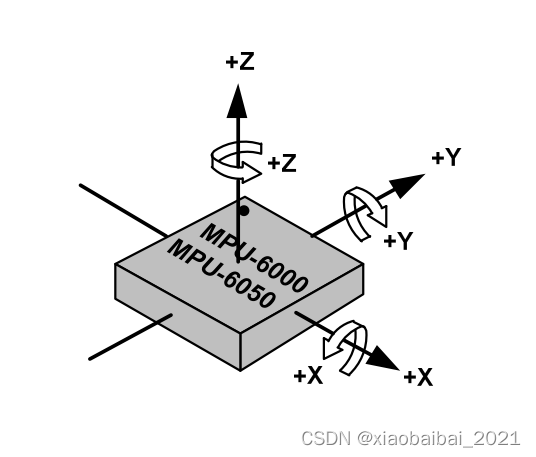
那么,滚转角(绕X轴转)和俯仰角(绕Y轴转)发生变化时,MPU6050测出来的重力加速度g的方向相对于载体也会发生变化。而加速度计测出来的重力加速度g的方向是实时的,不会受长时间计算累加的影响。所以,我们可以用加速度计测到的g的方向,来修正陀螺仪积分得到的滚转角和俯仰角。
而偏航角(绕Z轴转)变化时,MPU6050测到的重力加速度g方向是不会变化的,所以g的方向不能用来修正偏航角。要想修正偏航角,需要测量地磁偏角的传感器信息。
这个用加速度计或磁力计来修正姿态角的过程,一般称为数据融合,有多种方法实现。在之前的文章中,我们使用MPU6050芯片官方提供的DMP库直接获取了融合后的数据;但是这只适用于特定厂家的芯片,而更通用的方法是使用互补滤波或者卡尔曼滤波来实现,本节要讲的就是使用互补滤波的方法,来进行数据融合。
(注意,由于没有引入磁力计的数据,本文使用互补滤波的方法只是修正了俯仰角和滚转角的信息,无法修正偏航角,后续有机会再讲解如何用磁力计修正偏航角)
2)互补滤波的原理假如我们有两种途径测量某个信号,测得的结果一个带有高频噪声,一个带有低频噪声。我们为了获取更准确的信号,可以把它们的噪声分别滤掉,再合并,就得到了没有噪声的原始信号。具体操作如下图所示:
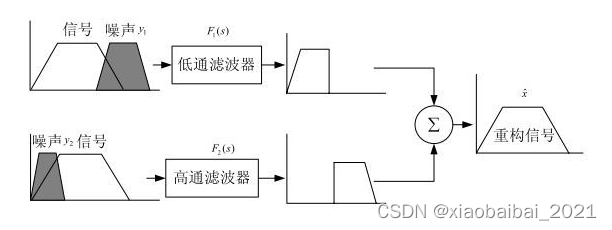
这就是互补滤波最基础的理论。
为了使得最后相加的重构信号与我们想要的信号尽量相等,一般要求F1(s) F2(s) = 1。
具体到我们的实际问题,姿态信息可以通过陀螺仪角速度积分得到,也可以通过加速度计实时测量得到;而且,陀螺仪积分得到的姿态主要包含低频噪声(零偏、累积误差),加速度计得到的姿态主要包含高频噪声。使用互补滤波正好可以融合二者的姿态信息。
依据上面这个框图,我们可以想到以下的姿态融合方法:
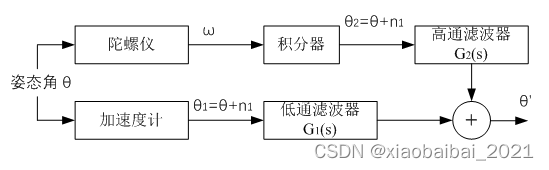
图中ω是角速度,n1和n2为噪声,θ’为融合后的角度。
当我们把滤波器简化为最简单的一个比例系数时,有如下形式:
姿态角 = k*陀螺仪姿态角 (1-k)*加速度计姿态角
(其中0<1,k的选择,取决于我们更相信陀螺仪的数据,还是更相信加速度计的数据)<>
你可能会很惊讶,这不就是个加权平均吗?就这也能滤波?
别急,它确实没有滤波,但我们先理解一下,再慢慢深入。
我们看看等式右边的两项,由于k小于1,所以陀螺仪姿态角的低频噪声被缩小了k倍;同样,1-k也小于1,所以加速度计姿态角的高频噪声被缩小了1-k倍;二者相加,姿态角的倍数仍为1,而高频和低频的噪声都被缩小了。虽然这个“滤波”效果有点弱,但是这样我们至少得到了一个高频、低频都比原始信号稍好一些的姿态信息,这就实现了高频和低频信号的互补。
实际上,当使用了有效的高通和低通滤波器时,噪声的影响会被进一步减弱。
前人的研究已经帮我们总结出了通用的公式,就是低通滤波器为LPF=C(s)/(C(s) s),高通滤波器HPF=s/(C(s) s)。选用不同的C(s)可以形成不同滤波效果。
把算法化成框图的形式,如下图所示:
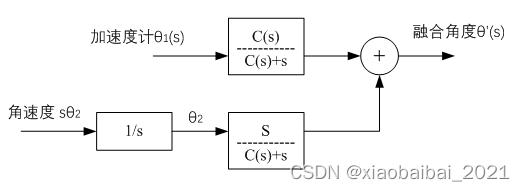
上面这个框图对于理解互补滤波的原理比较直观,但是等效为下图这种形式时,更接近于编程实现的思想:(有兴趣的可以推导一下,两种框图是等效的)
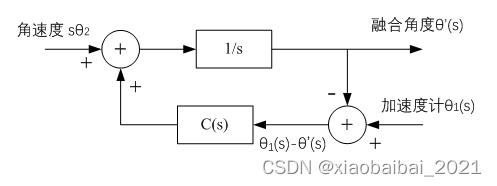
当选择不同的C(s)时,可以获得不同的滤波效果,C(s)为常数时,就是一阶滤波器;C(s)为a b/s时就是二阶滤波器。
3)互补滤波用于姿态融合的编程实现当求解姿态角时,必须要有一些四元数的知识,可以认为四元数等价于滚转角、俯仰角、偏航角。之所以要使用四元数,是因为它可以简化姿态更新的计算过程。基本上现在网上的开源代码都是以四元数来表征姿态角的。本文不去深究四元数的理论,只是拿来使用。
我们来看一下最经典互补滤波算法是如何实现的(这段代码被广泛应用在各种开源四轴飞行器上),它的核心部分如下:

ax、ay、az是加速度计测得的三个方向的加速度,gx、gy、gz是陀螺仪测得的三个方向的角速度。
首先,将ax、ay、az进行单位化,因为我们只需要使用它们求角度,不关心它们的大小,单位化的操作就是第65~68行,其中sqrt函数是求平方根:
然后,第72~74行,是依据当前的姿态来计算重力加速度;静止或匀速直线运动时,重力产生的加速度在地面东北天坐标系的xyz三个方向上分量是[0,0,g],再乘以姿态转换矩阵,就得到了机体坐标系下的加速度:
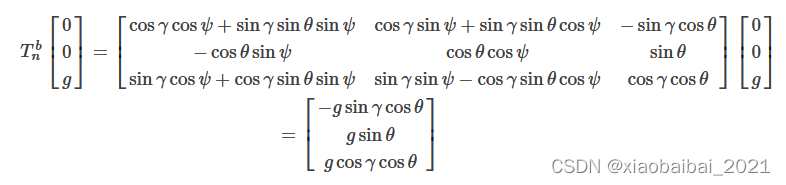
用四元数表示的姿态转移矩阵是:
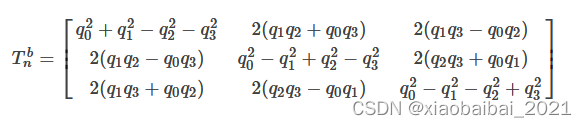
所以,转换矩阵的最后一列,就是在载体坐标系下的加速度(忽略了倍数g):
由于这个计算过程是通过已有的姿态转移矩阵算出来的,所以,它是包含了陀螺仪的角度信息的,那么它与加速度计的测量原始量ax、ay、az之间会比较接近但会有偏差。我们知道了这个偏差后,就可以用加速度计的测量值来修正已有的姿态了。
计算偏差的过程就是第77~79行,这里是用向量的外积(叉乘)作为向量之间的偏差:
注意,上一节的框图中,是通过角度θ1(s)-θ’(s)来计算偏差的,而这里的代码实现,是将θ’(s)反算到了三个轴的加速度vx、vy、vz之后,再计算三个轴的加速度误差,效果也是一样的,这样也是为了简化计算。
现在我们已经得到了框图中的θ1(s)-θ’(s)等效量ex、ey、ez,接下来就要选择合适的C(s)来确定滤波函数了。这部分代码中实现的,是使用的二阶滤波,取的C(s)=Kp Ki/s,也就是用“误差”和“误差的积分”共同去修正角速度,Kp和Ki是两个由用户确定的常数,代码如下:
细心的朋友可能发现了,这与PID控制中只使用了PI环节是一样的,有比例项和积分项。所以,代码里也用Kp和Ki两个参数来表示,这两个参数都是需要调试的。
执行完这里,就已经完成了加速度计对陀螺仪的修正。上一节的框图就只剩下最后一步,积分一次就能得到新的姿态角了。
我们使用四元数更新姿态时,不是使用积分累加的方法,而有另一种方法:
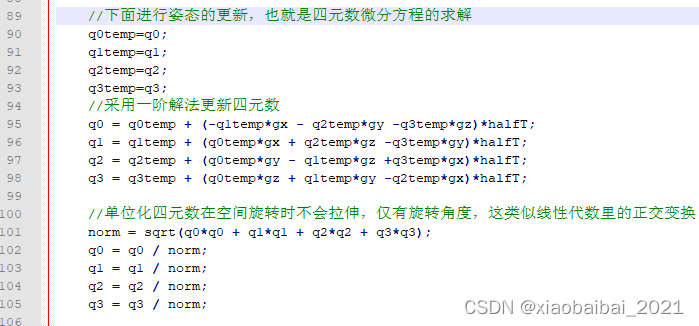
具体为什么如上面计算用角速度和周期可以更新四元数,这里不深入探讨了,有兴趣可以找资料深入了解。
最后,有需要的话,可以用更新后的四元数,通过反三角函数来求取当前的姿态角:

互补滤波的这段代码,在使用时,只要周期性地获取陀螺仪和加速度计的数据、调用互补滤波函数、更新四元数、计算姿态角即可。
最后,测试一下互补滤波的效果,取Kp=10,Ki=0.008,初始时z轴向上保持5s进行MPU6050传感器自校正,然后每100ms获取一次MPU6050的测量数据,进行互补滤波,计算姿态角,送到上位机显示。
可以看到,经过较长时间后,俯仰和滚转角都可以保持正确,不会产生误差累积和漂移,说明陀螺仪的数据得到了加速计的修正;而偏航角是不能实时修正的,会慢慢越偏越大:
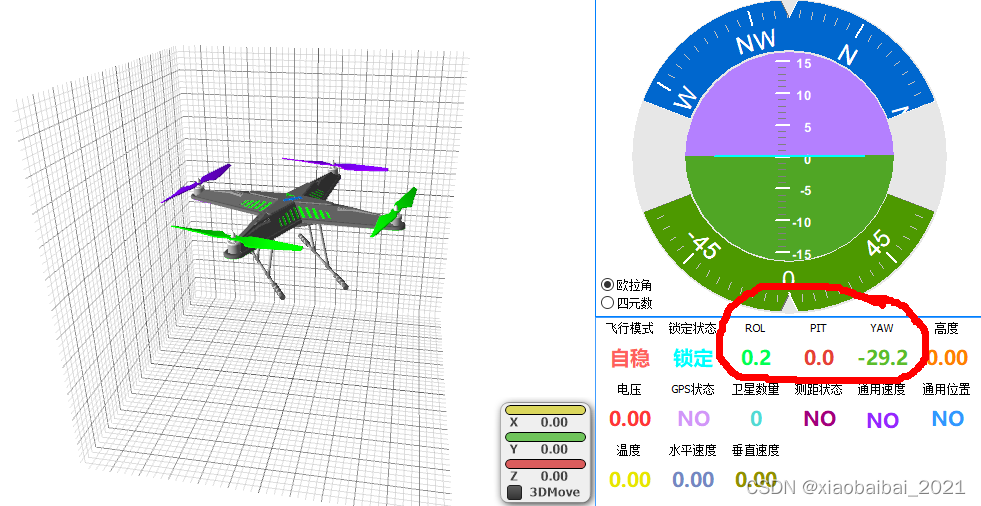
好了,关于互补滤波姿态融合的知识,就讲到这里了。

 扫码关注
扫码关注