扫码关注
上一节我们分析了使用比较器产生方波和正弦波的电路，其本质上是在电容充放电的一段延时后，利用比较器产生电平翻转。而本节分析的正弦波产生电路，产生的原理不同。
1）振荡产生的原理
正弦波产生电路，原理如下图所示：
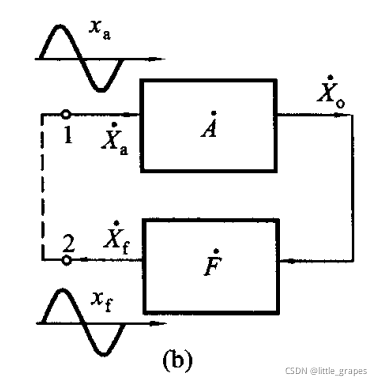
由放大电路、反馈电路组成，形成一个回路，从放大电路的输出作为电路的总输出。
一般要求在放大电路和反馈回路中，经过一个回路放大后，增益大于1，而且有一定的延时。增益大于1，可以使得外部的扰动或者电路自身初始的不稳定信号放大，得到初始激励；经过绕环路一周，延时使得相位变化后，满足延时整数倍周期的信号回到放大电路A处时，会再次放大，相位相同的信号得到正反馈，这个过程可以看做电路对频率的选择作用，所以称为选频网络；如此不断循环，特定频率的信号幅值越来越大，最终达到稳定，实现自行振荡的作用。
2）RC正弦波振荡电路
原理如下图：
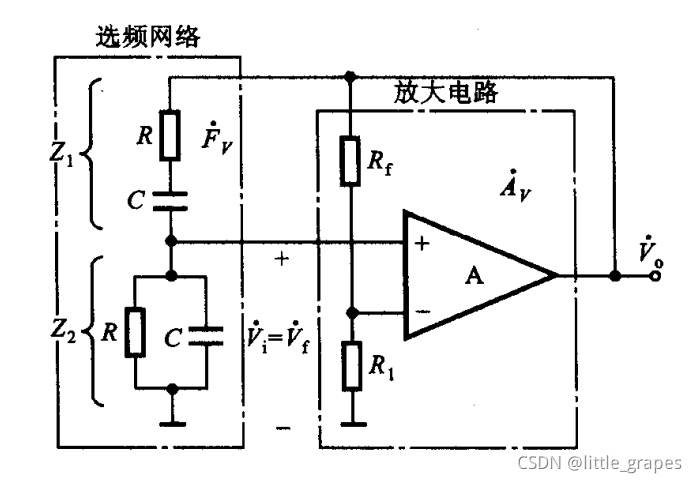
图中，左侧的RC在充放电时，会使得信号产生延时，构成选频网络；右侧的放大器形成同相比例放大电路。
列出选频网络部分的拉普拉斯方程：
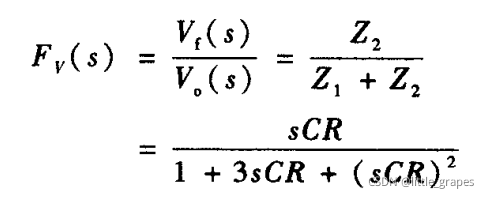
可以求出，当 ω = 1/RC 时，幅频响应最大，反馈系数Fmax = 1/3，相频响应为0。也即是当取 ω = 1/RC 时，输出电压幅值最大，而且没有相位差；此时Vf = Vo/3，也就是说图中 Rf 应该选择为 R1 的两倍，使得放大电路将Vf放大3倍得到Vo，才能建立稳定的振荡。
以上是振荡稳定后的状态，对选频后的信号是不放大的。但在实际工程中，设计电路时，为了初始时能够起振，需要把放大电路的放大倍数设置得大于3，才能从初始的杂波中一步步将选频网络选中的波形放大，一般来说放大倍数越大越容易启振。
但是，从理论分析看，放大倍数大于3时，是不能稳定的，信号幅值会越来越大。直到达到运放输出的最大幅值，产生非线性失真。而此时信号不会是标准的正弦波。
仿真电路图如下：
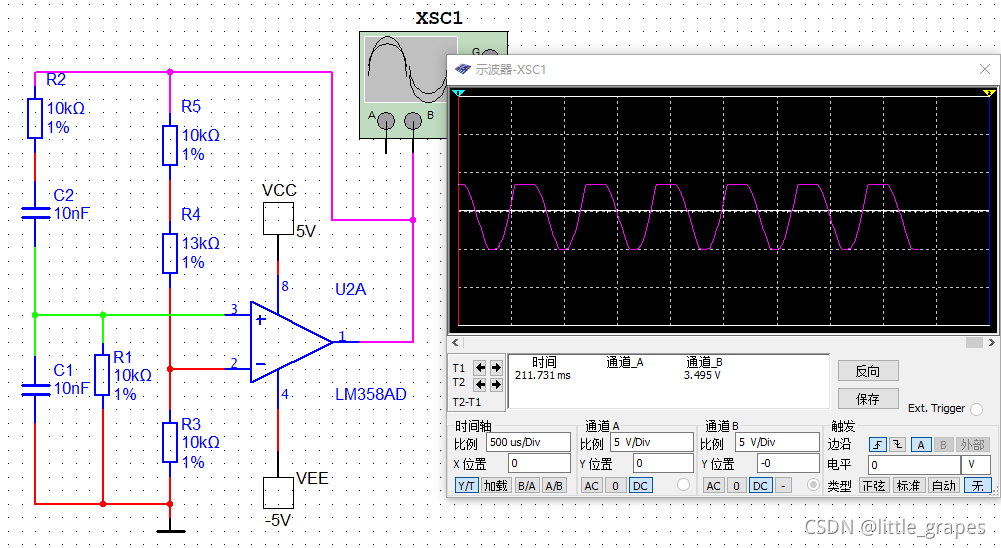
这里放大倍数为33/10，略大于3，可以起振；但是可以看到，最终稳定后的波形有失真，不是标准的正弦波。
为了减少失真，可以减小放大倍数，如设置为放大倍数为3.1，失真会变小，如下图：
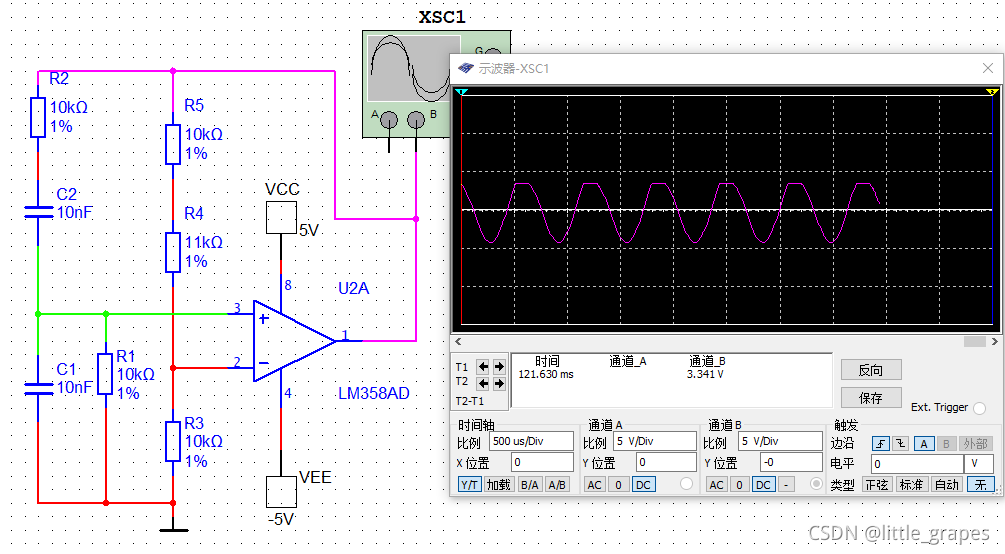
但是，放大倍数变小会使得起振到稳定的时间变长。而且失真是始终会存在的，只能减小不能消除。
还有一种方法可以减小失真至几乎没有，就是使用非线性器件，如下图增加两个二极管：
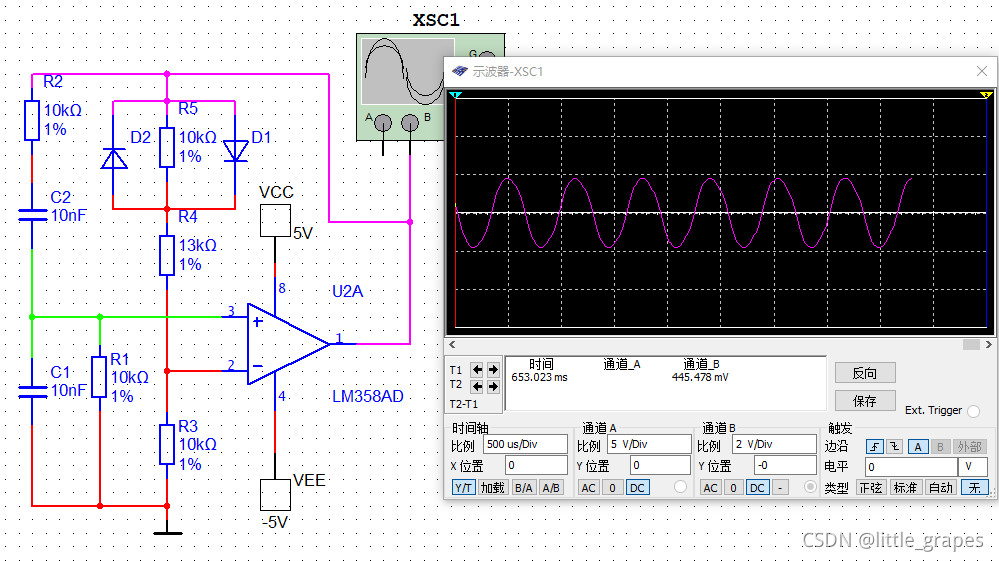
该电路分析如下：在刚起振时，输出幅值很小，经电阻分压到二极管上的电压也很小，二极管不导通，所以放大倍数大于3；一定的时间后，输出幅值变大后，二极管能够导通时，则放大倍数会减小；当放大倍数减小到等于3时，达到平衡，振荡波形稳定。这样输出的波形为近似标准的正弦波。
由于运放的带宽限制，一般RC和运放组成的正弦波振荡电路，只适用于产生频率较低的波形，如1MHz以下时使用较为合适。
PS：记录一个小技巧，在使用multsim仿真软件时，运放要选择“5 Terminal Opamp Model”类型的器件。如果选择了“3 Terminal Opamp Model”的运放，它会不受电源的限制，输出幅值可能会超出电源范围。
