本节我们来分析LC正弦波产生电路,它与前面讲的RC正弦波振荡电路的基本原理是一样的,都是由选频网络、放大电路组成;区别是LC正弦波振荡电路的选频网络是由电感L和电容C组成的。
LC正弦波振荡电路工作的频率一般比RC振荡电路高,通常在1MHz以上。
1)LC并联谐振回路
首先我们来分析选频网络,一般使用LC并联谐振回路作为选频网络。我们知道,当外部的信号与LC并联电路特征频率相等时,能产生谐振,信号幅值能达到最大,这样就能选择出我们需要频率的信号。
LC并联谐振回路的原理图如下,图中R表示回路的等效损耗电阻:

由图可知,电路的等效阻抗为:
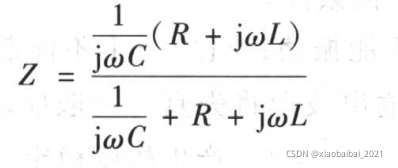
由于R远小于ωL,所以有:
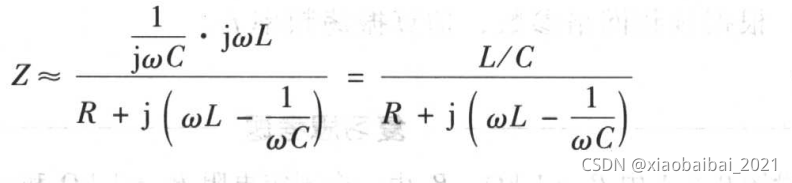
所以,当ω取如下值时,回路谐振,呈现纯电阻特性
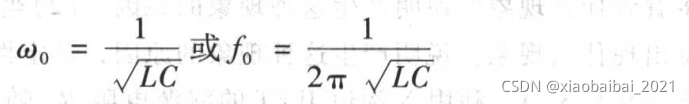
而且,此时其等效阻抗为:
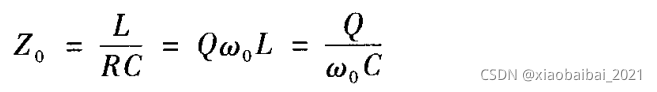
一般Z0是一个比较的大电阻值,理想状态下是无穷大。
Q=ω0L/R称为品质因数,用于评价回路损耗的大小。通常Q值很大,在几十到几百范围。Q值越大,对频率的选择特性越好。
此外由于R一般很小,谐振回路内部的电流会远大于外部输入的电流,即上图中的Ic和IL的绝对值要远大于Is。
2)变压器反馈式LC振荡电路
变压器反馈式LC振荡电路,顾名思义,它是利用了变压器耦合进行反馈的电路,原理如下图:
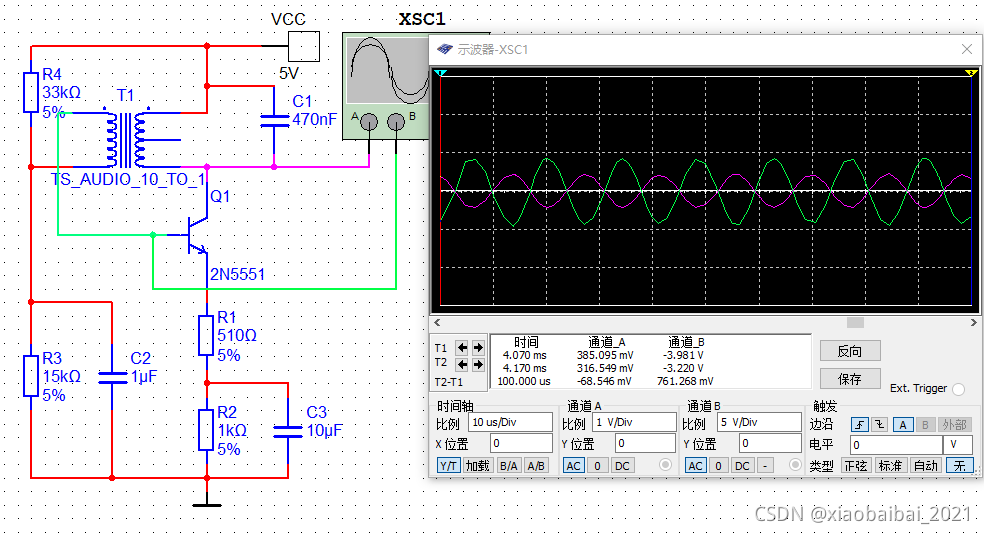
这个电路分析如下:
C1和变压器的T1的一端形成LC并联谐振电路,作为选频网络;当电路谐振时,等效于一个纯电阻;
三极管的电路形式为共射级放大,其输出(集电极)和输入(基极)的相位是相反的;
注意变压的同名端,当输出(集电极)电压升高时,使得基极的电压会降低,从而形成了正反馈,因此可以不断放大振荡信号。
3)电感三点式振荡电路
电感三点式振荡电路,又称为电感反馈式振荡电路,仿真图如下:
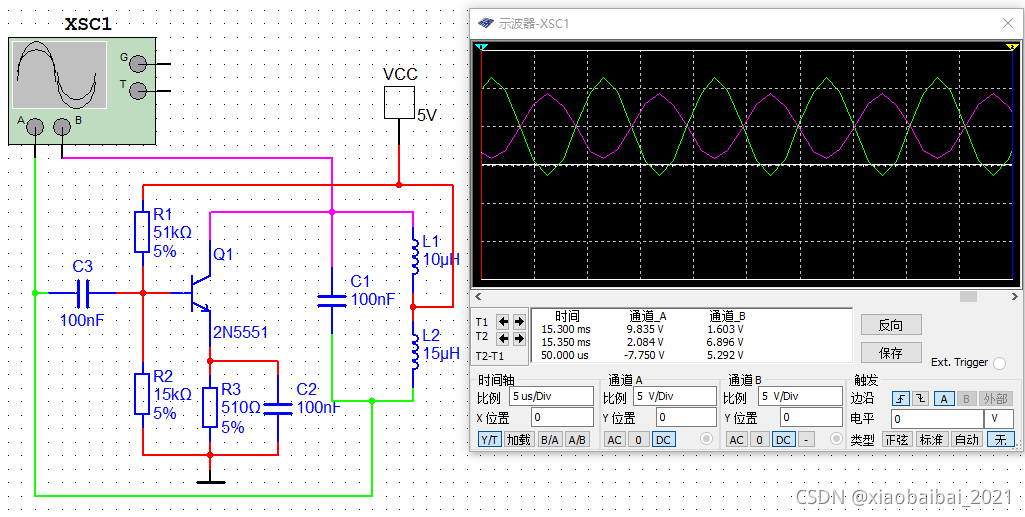
这个电路分析如下:
由于谐振时,回路内部的电流远大于外部输入的电流;所以谐振回路的两端可以看做相位相反;而三极管的共射放大电路,也有反相作用;两个反相叠加后形成了正反馈。
它的振荡频率为:(其中M为两个电感间的互感)
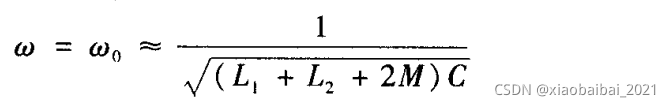
4)电容三点LC式振荡电路
电容三点式LC振荡电路,又称为电容反馈式振荡电路,仿真图如下:
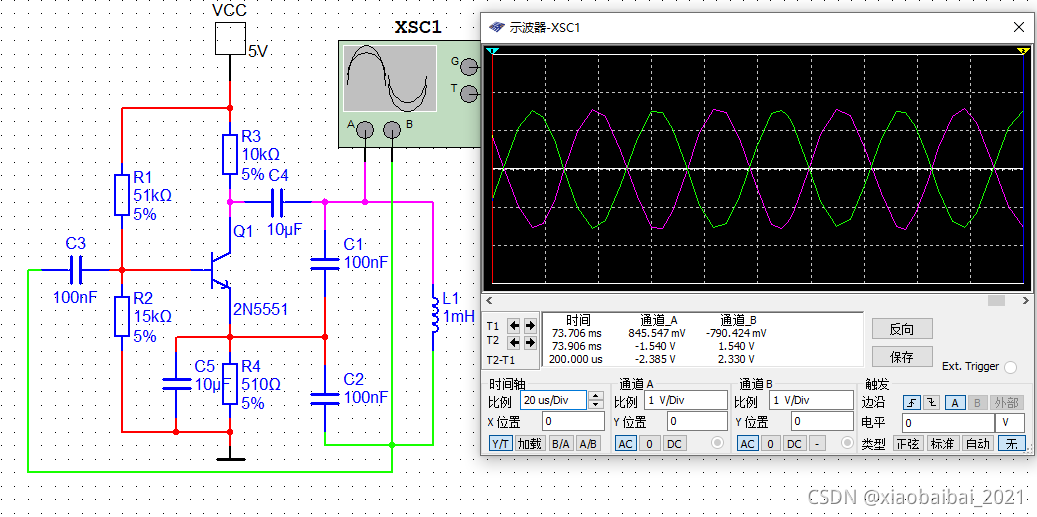
这个电路分析与电感三点式很相似:
由于谐振时,回路内部的电流远大于外部输入的电流;所以谐振回路的两端可以看做相位相反;而三极管的共射放大电路,也有反相作用;两个反相叠加后形成了正反馈。
它的振荡频率为:
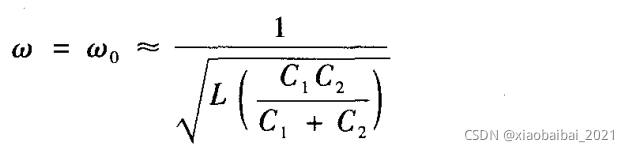
这个电路的缺点是,当需要调节C1和C2的值来改变频率时,反馈系数也会改变。所以一般使用如下改进型电路,在L上并上一个可变电容,这样就可以只调节可变电容改变频率,而不影响反馈系数。
5)改进型的电容反馈式振荡电路
为了提高振荡电路的稳定性,可以使用如下克拉波电路:

这个电路相当于电容三点式电路中,L上串联了一个小电容C3;由于C3远小于C1和C2,所以振荡回路的选频特性主要由L和C3决定;这样减弱了晶体管与振荡回路的耦合,使得有源器件对振荡回路的影响变小,提高了频率稳定度。
6)总结:LC三端式振荡器相位平衡调节的判断
上述讨论的LC三端式振动器可以化成下图的等效形式:
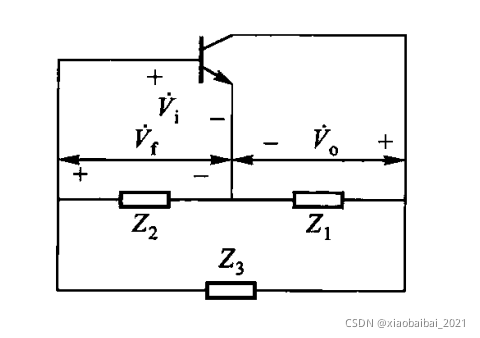
显然,如果要产生谐振,必须满足Z1 Z2 Z3 = 0;当回路电阻R很小时,近似为纯电抗,即满足:X1 X2 X3=0。
另外,为了满足相位条件,Vo与Vf需相差180°,这样再经过三极管的反相放大以后能形成正反馈,则X1和X2必须为同一性质的电抗,如都为电容、或者都为电感,而X3为另一种电抗。
好了,振荡电路到这里基本到一段落了。

 扫码关注
扫码关注