文氏振荡电路(Wien Bridge Oscillator Circuit),是一种基于正反馈原理的振荡电路,广泛用于产生稳定且可调频的正弦波信号。其结构独特,能够在较宽的频率范围内实现稳定的振荡,因此在无线电收发机、音频放大器及电子钟等广泛应用。
1、文氏振荡电路有哪些组成结构?
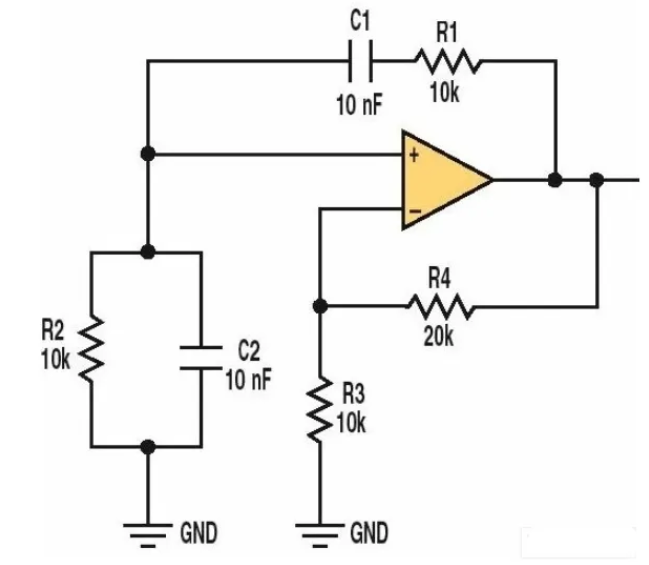
如图所示,文氏振荡电路主要由以下几部分组成:
放大器:提供信号的放大功能。
正反馈网络:由R1、R2、C1、C2组成的RC串并网络,将输出信号正反馈至放大器的同相输入端。
选频网络:由R1、R2、C1、C2组成的网络同时起到选频作用,决定振荡频率。
稳幅电路:通常由二极管D1、D2等非线性元件组成,用于稳定输出信号的幅度。
2、文氏振荡电路的工作原理是什么?
初始状态:电桥平衡时,满足R1C1 = R2C2且C3 + C4 = C1 + C2。此时,若存在微小的扰动信号,该信号将被放大器放大并送入反馈网络。
正反馈:当反馈网络中的相位移动为360度时,输出信号与输入信号的相位差为0度,形成正反馈。正反馈导致输出信号不断增大,直至放大器达到饱和状态或其他非线性效应出现。
选频:输出信号的频率由选频网络决定,该网络能够选出特定频率的信号进行振荡。
稳幅:利用二极管的非线性特性实现稳幅。当输出信号较小时,二极管截止;随着振荡信号振幅的增大,二极管在交替出现的输出波形峰值处导通,从而限制振荡的最大幅度。
3、如何分析文氏振荡电路?
检查电桥平衡条件:确保R1C1 = R2C2且C3 + C4 = C1 + C2,以满足振荡条件。
分析正反馈网络:观察正反馈网络是否将输出信号正确反馈至放大器的同相输入端,并检查相位移动是否为360度。
计算振荡频率:根据R1、R2、C1、C2的数值,计算振荡频率。
分析稳幅电路:检查二极管D1、D2等非线性元件是否正确连接,并理解其稳幅原理。
本文凡亿教育原创文章,转载请注明来源!

 扫码关注
扫码关注