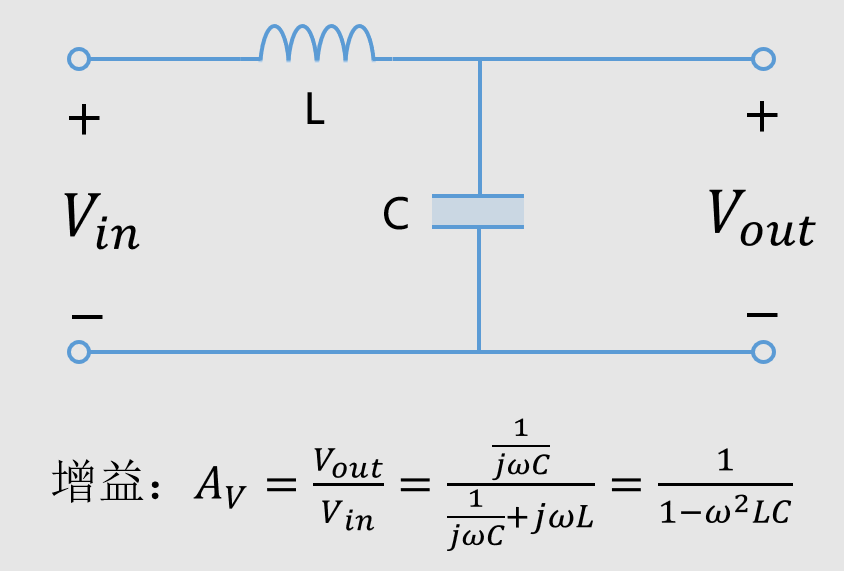
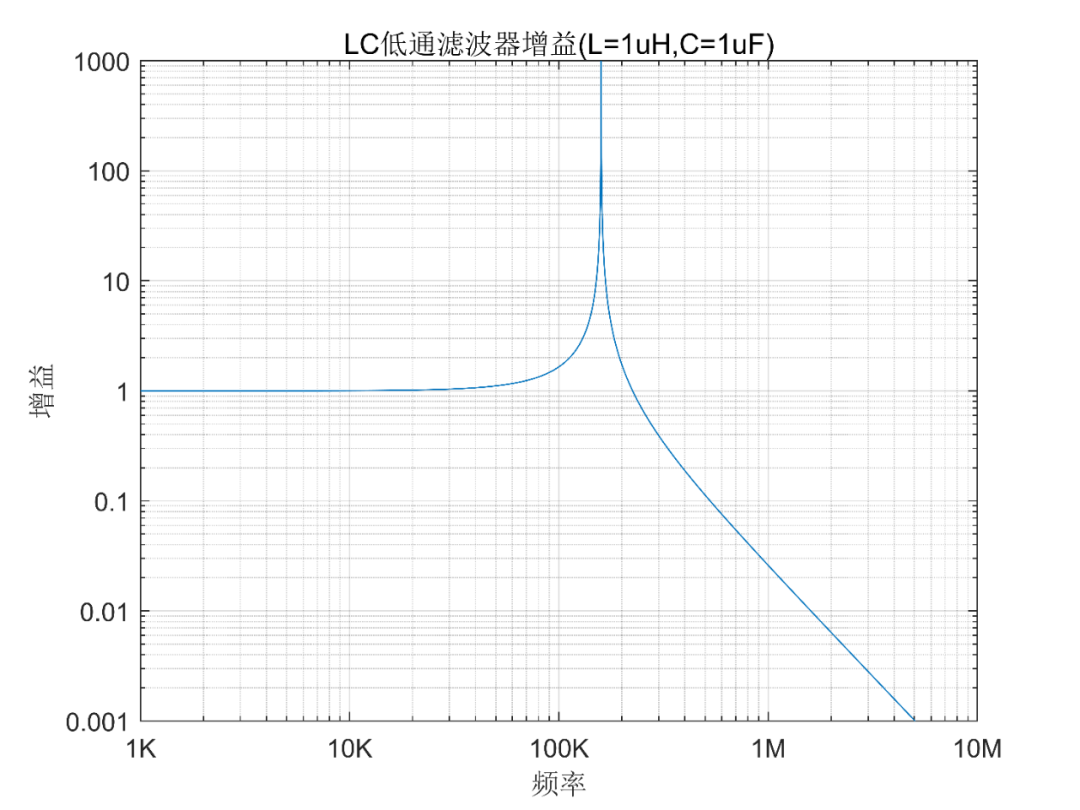
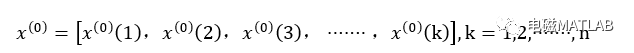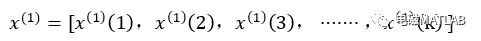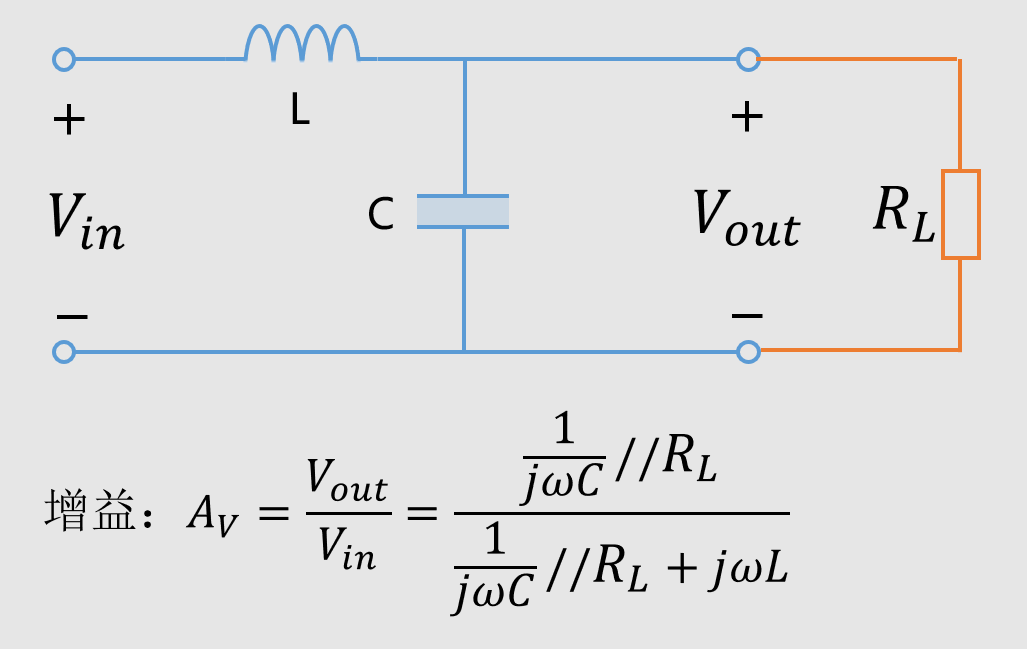1 CMAC概述
小脑模型神经网络(Cerebellar Model Articulation Controller,CMAC)是一种表达复杂非线性函数的表格查询型自适应神经网络,该网络可通过学习算法改变表格的内容,具有信息分类
存储的能力。
CMAC把系统的输入状态作为一个指针,把相关信息分布式地存人一组存储单元中。它本质上是一种用于映射复杂非线性函数的查表技术。具体做法是将输入空间分成许多分块,每个分块指定一个实际存储器位置;每个分块学习到的信息分布式地存储到相邻分块的位置上;存储单元数通常比所考虑问题的最大可能输入空间的分块数少得多,故实现的是多对一的映射,即多个分块映射到同样一个存储器地址上。CMAC已被公认为是一类联想记忆神经网络的重要组成部分,它能够学习任意多维非线性映射,CMAC算法可有效地用于非线性函数逼近、动态建模、控制系统设计等。CMAC较其他神经网络的优越性体现在:①它是基于局部学习的神经网络,它把信息存储在局部结构上,使每次修正的权很少,在保证函数非线性逼近性能的前提下,学习速度快,适合于实时控制;②具有一定的泛化能力,即所谓相近输入产生相近输出,不同输入给出不同输出;③连续(模拟)输入、输出能力;④寻址编程方式,在利用串行计算机仿真时,它可使回响速度加快;⑤作为非线性逼近器,它对学习数据出现的次序不敏感。由于CMAC所具有的上述优越性能,使它比一般神经网络具有更好的非线性逼近能力,更适合于复杂动态环境下的非线性实时控制。CMAC的基本思想在于:在输入空间中给出一个状态,从存储单元中找到对应于该状态的地址,将这些存储单元中的内容求和得到CMAC的输出;将此响应值与期望输出值进行比较,并根据学习算法修改这些已激活的存储单元的内容。CMAC的结构如图8-5所示。
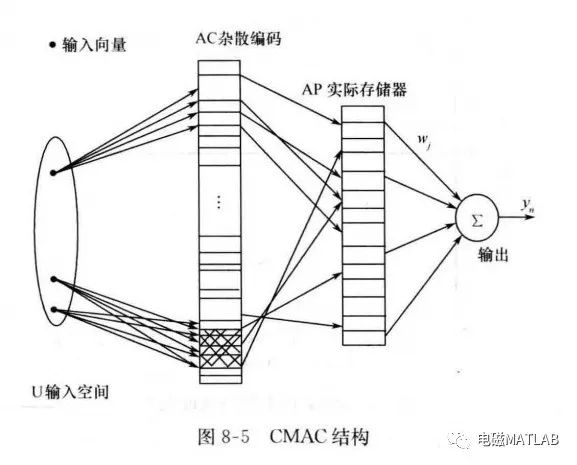
2 一种典型CMAC算法
CMAC网络由输入层、中间层和输出层组成。在输入层与中间层、中间层与输出层之间分别为由设计者预先确定的输入层非线性映射和输出层权值自适应性线性映射。在输人层对维输人空间进行划分。中间层由若干个基函数构成,对任意一个输入只有少数几个基函数的输出为非零值,称非零输出的基函数为作用基函数,作用基函数的个数为泛化参数c,它规定了网络内部影响网络输出的区域大小。中间层基函数的个数用M表示,泛化参数c满足c《M。在中间层的基函数与输出层的网络输出之间通过连接权进行连接,采用梯度下降法实现权值的调整。CMAC神经网络的设计主要包括输人空间的划分、输入层至输出层非线性映射的实现及输出层权值学习算法。CMAC是前馈网络,输入与输出之间的非线性关系由以下两个基本映射实现。
2.1 概念映射(U→AC)
概念映射是从输入空间U至概念存储器AC的映射。考虑单输入映射至AC中c个存储单元的情况。取u(k)作为网络的输入,采用如下线性化函数对输入状态进行量化,实现CMAC的概念映射
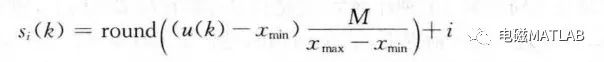
式中,xmax和xmin为输入的最大、最小值,M为xmax量化后所对应的初始地址,round()为四舍五入Matlab函数,i=1,2,…,c。由式(8.9)可见,当u(k)为xmin时,u(k)映射地址为1,2,…,c;当u(k)为xmax时,u(k)映射
地址为M 1,M 2,…,M c。
映射原则为:在输入空间邻近的两个点在AC中有部分的重叠单元被激励。距离越近,重叠越多;距离越远,重叠越少。这种映射称为局部泛化,c为泛化常数。
2.2 实际映射(AC→AP)
实际映射是指由概念存储器AC中的c个单元映射至实际存储器AP的c个单元,c个单元中
存放着相应权值。网络的输出为AP中c个单元的权值的和。
采用杂散编码技术中除留余数法实现CMAC的实际映射。设杂凑表长为m(m为正整数),
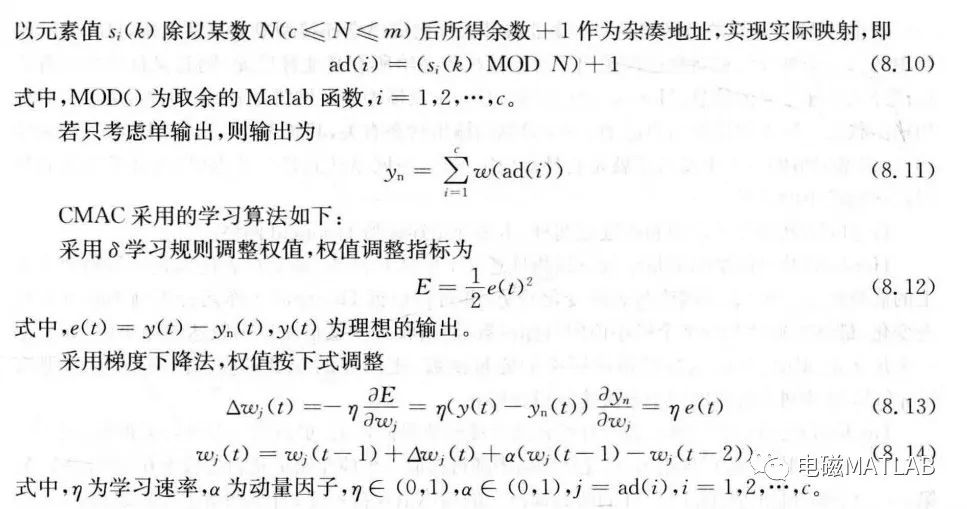
3 算例
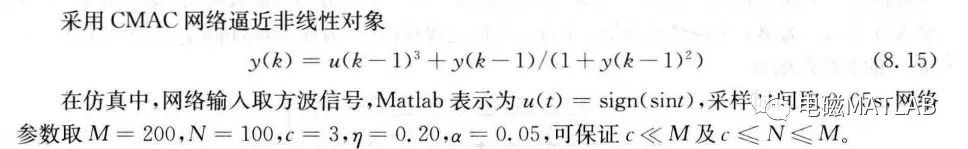
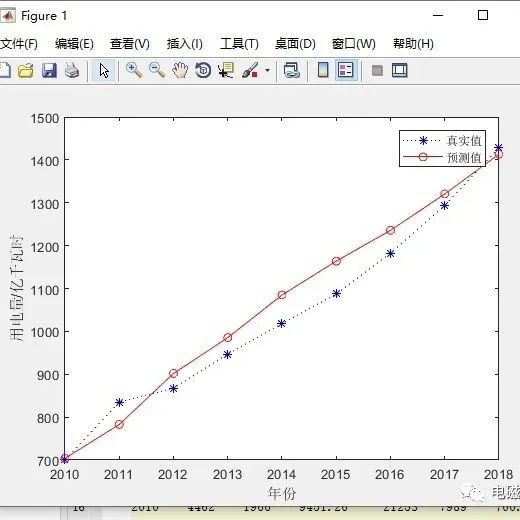
4 验算结果
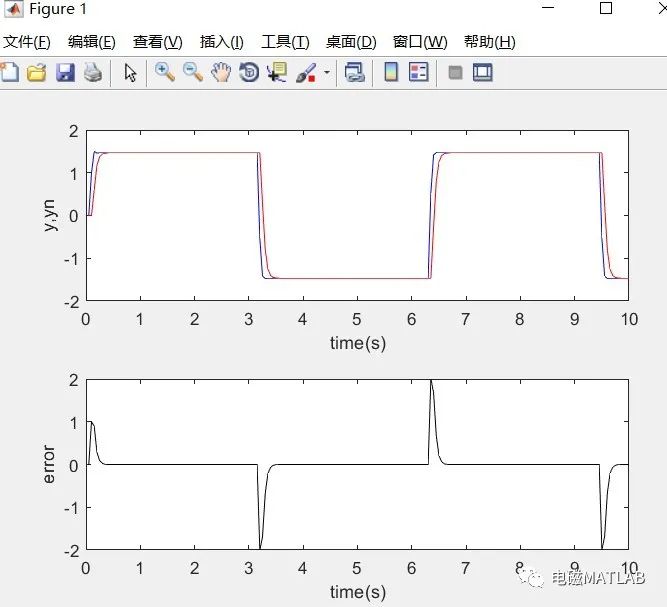
6 程序
%CMAC Approximation for nonlinear modelclcclear;close all;%学习效率xite=0.20;%动量因子alfa=0.05;
M=200;N=100;c=3;%权重值w=zeros(N,1);w_1=w;w_2=w;d_w=w;%初始状态u_1=0;y_1=0;ts=0.05;for k=1:1:200time(k)=k*ts;%% 输入层u(k)=sign(sin(k*ts));
xmin=-1.0; xmax=1.0;%% 概念映射与实际映射for i=1:1:c s(k,i)=round((u(k)-xmin)*M/(xmax-xmin)) i; %Quantity:U-->AC ad(i)=mod(s(k,i),N) 1; %Hash transfer:AC-->APend
sum=0;for i=1:1:c sum=sum w(ad(i));end%% 输出层yn(k)=sum;y(k)=u_1^3 y_1/(1 y_1^2); %Nonlinear model%% 跟踪误差error(k)=y(k)-yn(k);%% 权重调整for i=1:1:c ad(i)=mod(s(k,i),N) 1; j=ad(i); d_w(j)=xite*error(k); w(j)=w_1(j) d_w(j) alfa*(w_1(j)-w_2(j));end%% 迭代更新%%%% Parameters Update %%%%w_2=w_1;w_1=w;u_1=u(k);y_1=y(k);endfigure(1);subplot(211);plot(time,y,'b',time,yn,'r');xlabel('time(s)');ylabel('y,yn');subplot(212);plot(time,error,'k');xlabel('time(s)');ylabel('error');

 扫码关注
扫码关注