1 静止两相正交坐标系中的动态数学模型
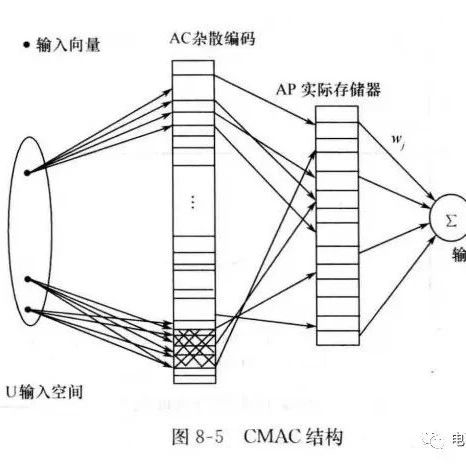
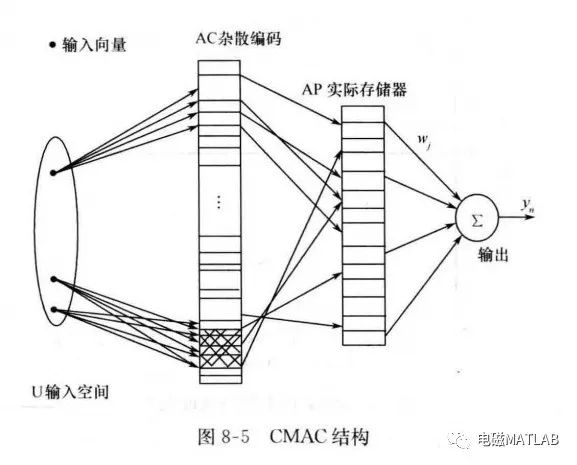
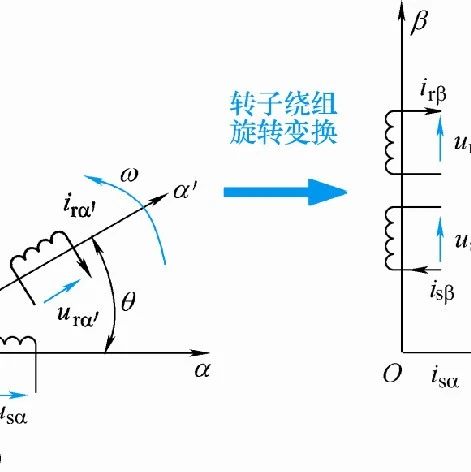
1.1 定子绕组和转子绕组的3/2变换
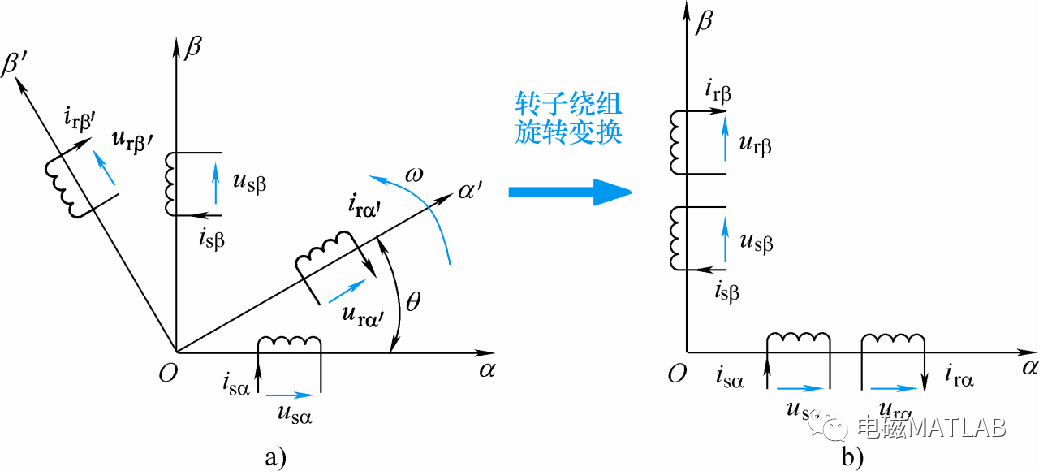
对静止的定子三相绕组和旋转的转子三相绕组进行相同的3/2变换,变换后的定子两相正交坐标系静止,而转子两相正交坐标系以角速度逆时针旋转。
1.2 电压方程
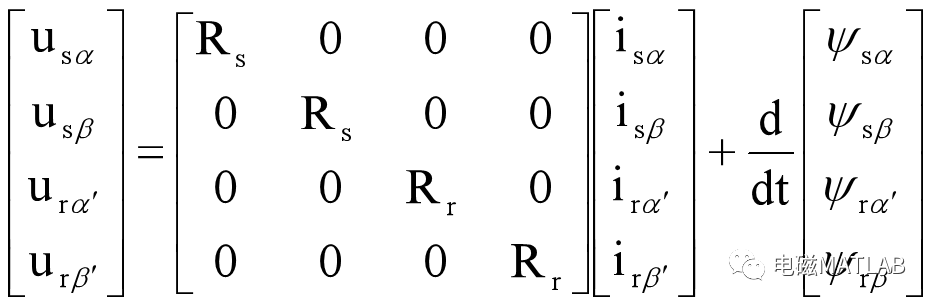
1.3 磁链方程
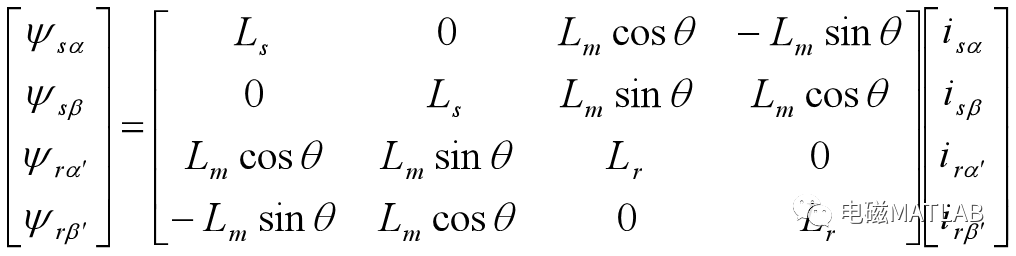
1.4 转矩方程
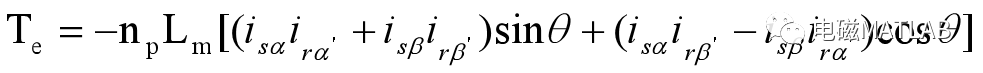
2 静止两相正交坐标系中的状态方程
三相感应电机在三相坐标系上的状态方程是8阶方程,其中6阶电压方程、1阶运动方程和1阶转角方程由前述两相坐标系中的动态方程可见,如果不计零序分量,两相坐标系上的电压方程为4阶,加上1阶运动方程,其状态方程降为5阶,由于电感矩阵与转角6无关,转角方程可以不必列于联立求解的微分方程组感应电机的状态方程可以建立在不同的两相坐标系上,而且状态变量也有不同的选取方法,除了转速作为必选的状态变量外,其余4个状态变量可以在两相定子电流、两相转子电流、两相定子磁链、两相转子磁链这4组变量中任意选取两组。将两相静止坐标系上的磁链方程代入到电压方程中,写成矩阵形式可得:
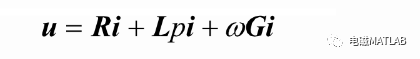
其中:
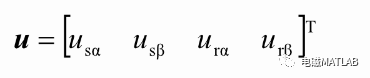
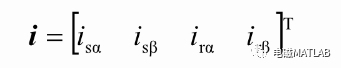
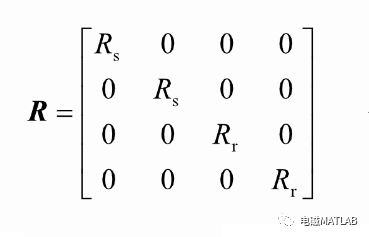
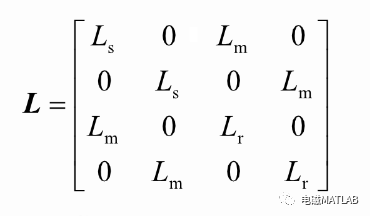
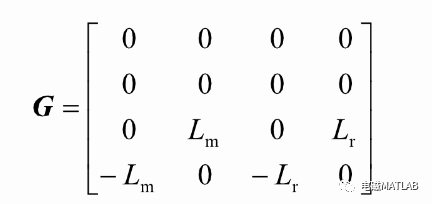
则
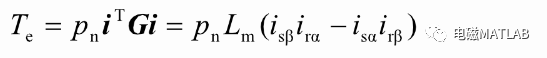
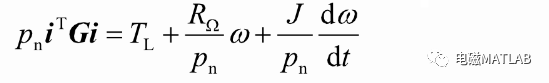
整理得:
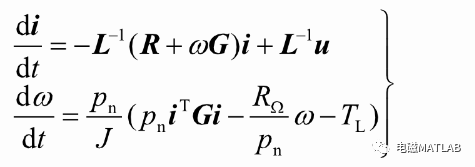
3 算例电机参数如下:f=50;Un=220;Rs=2.68;Rr=2.85;LAA=0.265;Laa=0.265;Lms=0.253;pn=2;J=0.02;ROmega=0;TL=0;
4 程序运行结果
电流
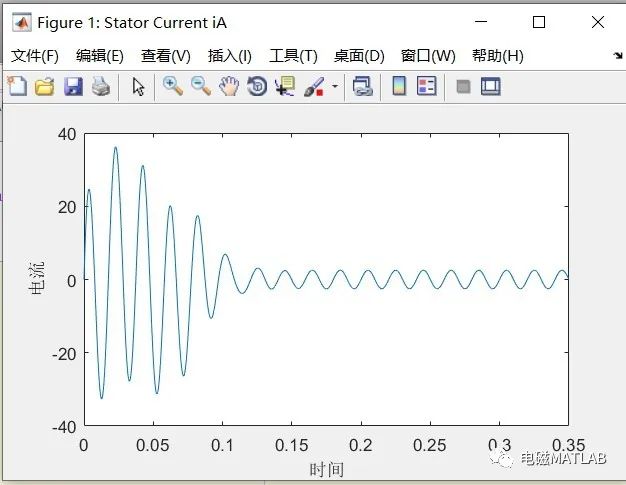
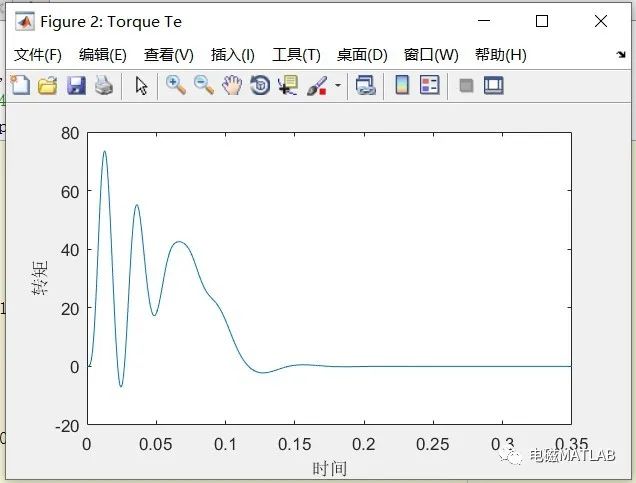
转矩
转速-转矩
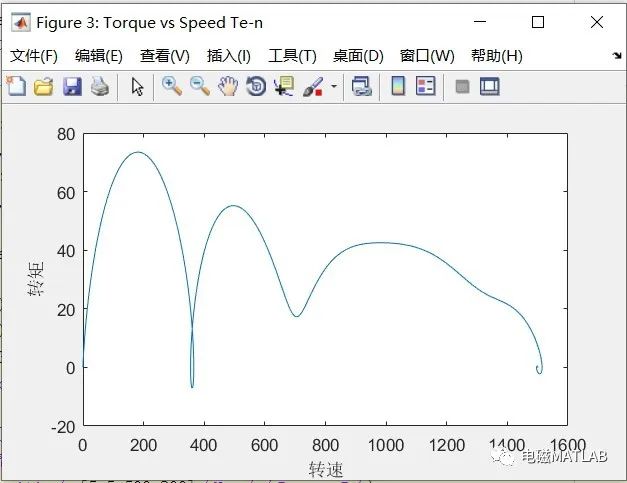
5 matlab程序
1)主函数
clcclearclose all%% 参数f=50;Un=220;Rs=2.68;Rr=2.85;LAA=0.265;Laa=0.265;Lms=0.253;pn=2;J=0.02;ROmega=0;TL=0;%计算两相坐标系电感Lm=3*Lms/2;Ls=LAA-Lms Lm;Lr=Laa-Lms Lm;%% 计算电感矩阵LL=[ Ls,0,Lm,0; 0,Ls,0,Lm; Lm,0,Lr,0; 0,Lm,0,Lr ];%% 电阻矩阵R=[Rs,0,0,0; 0, Rs,0,0; 0,0,Rr,0; 0,0,0,Rr ];%% 计算G矩阵G=[0,0,0,0; 0,0,0,0; 0,Lm,0,Lr; -Lm,0,-Lr,0 ];%% 计算L的逆L_INV=inv(L);%% 仿真y0=zeros(5,1);TF=0.35;options=odeset('RelTol',1e-3,'AbsTol',1e-4,'MaxStep',1e-3);%调用变步长龙格库塔法ode45求解[T,Y]=ode45(@IM_Model_2ph,[0,TF],y0,options,f,Un,R,L_INV,G,pn,J,ROmega,TL);%% 结果输出is_alpha=Y(:,1);is_beta=Y(:,2);ir_alpha=Y(:,3);ir_beta=Y(:,4);%计算转矩Te=pn*Lm*(is_beta.*ir_alpha-is_alpha.*ir_beta);%画图iA=sqrt(2/3)*is_alpha;Omega=Y(:,5);n=Omega/pn*30/pi;h=figure('Position',[520,380,500,300],'Name','Stator Current iA');plot(T,iA)xlabel('时间')ylabel('电流')h=figure('Position',[5,5,500,300],'Name','Torque Te');plot(T,Te)xlabel('时间')ylabel('转矩')h=figure('Position',[520,5,500,300],'Name','Torque vs Speed Te-n');plot(n,Te)xlabel('转速')ylabel('转矩')
2)子函数
function dy=IM_Model_2ph(t,y,f,Un,R,L_INV,G,pn,J,ROmega,TL)i=y(1:4);Omega=y(5);dy=zeros(5,1);Um=Un*sqrt(2);ANG=2*pi/3;%% 定转子绕组电压向量uABC=Um*[cos(2*pi*f*t); cos(2*pi*f*t-ANG); cos(2*pi*f*t ANG)];C3_2=sqrt(2/3)*[1,-1/2,-1/2; 0,sqrt(3)/2,-sqrt(3)/2];us=C3_2*uABC;u=[us; 0; 0];dy(1:4)=L_INV*(-(R Omega*G)*i u);dy(5)=pn/J*(pn*i'*G*i-ROmega*Omega/pn-TL);
end

 扫码关注
扫码关注