直流潮流计算matlab程序

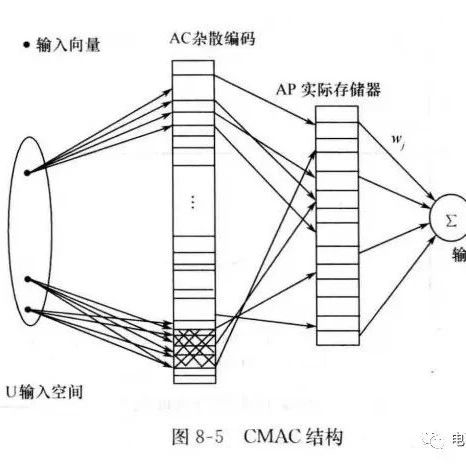
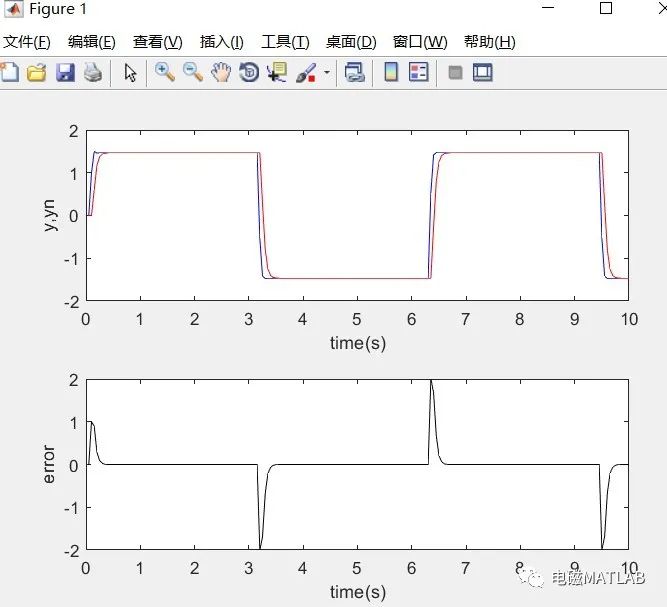
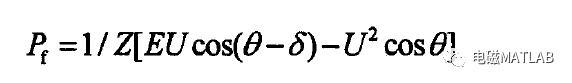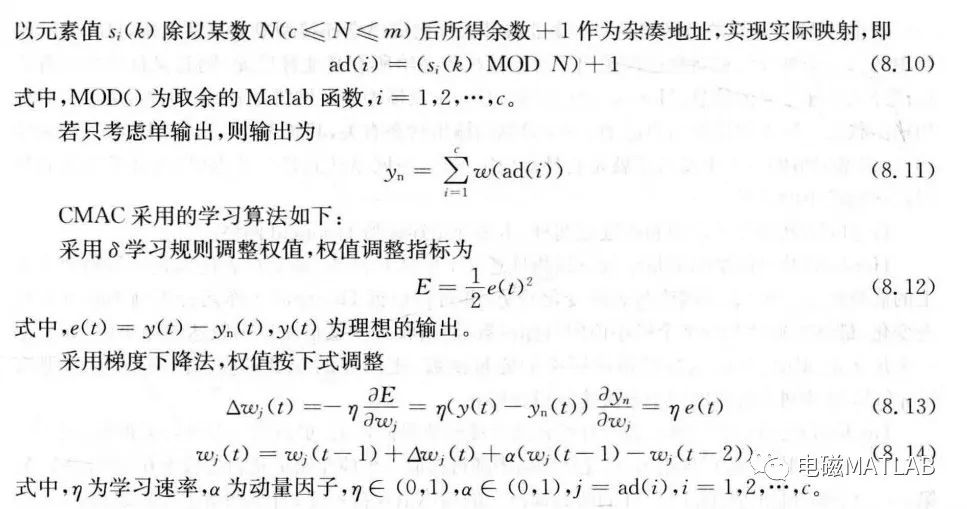一、直流潮流计算原理

直流潮流的特点是用电力系统的交流潮流（有功功率和无功功率）等值的直流电流来代替。甚至只用直流电路的解析法来分析电力系统的有功潮流，而不考虑无功分布对有功的影响。这样一来计算速度加快，但计算的准确度有所降低，本方法适用于对潮流计算准确度要求不高的计算场景。

下面先对直流潮流法的原理进行简单介绍：

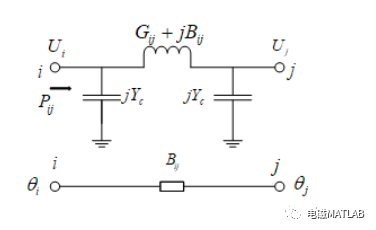
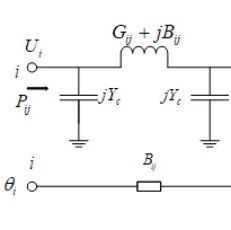
上图为直流法的等值图，在上图所示的输电线路中，有功潮流为：

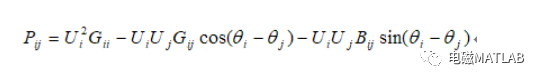
为了快速计算的需要，将上式进行了三项简化：
（1）考虑一般高压电网中线路的电阻远小于电抗，对地电导也可以忽略即 Gii=0 Gij =0
（2）按照标幺值计算时，节点电压与其额定电压相差不大，故有：Ui≈Uj≈1.0；
（3）线路两端的电压相角差（θi-θj）较小，所以有：

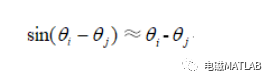
这样，上式前两项均为零，只剩第三项

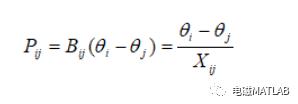
这就相当于线路两端的直流电位分别为θi和θj。线路的直流电阻是Xij。则用矩阵表示为如下式所示。

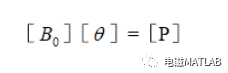
式中：B0为正常运行时网络的节点电纳矩阵；θ为网络中各节点的电压相位角的向量；P为节点注入的有功功率向量。

二、算例

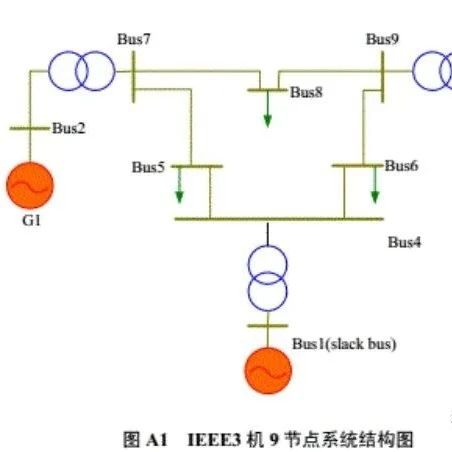
以IEEE9节点系统为算例，系统参数如下。
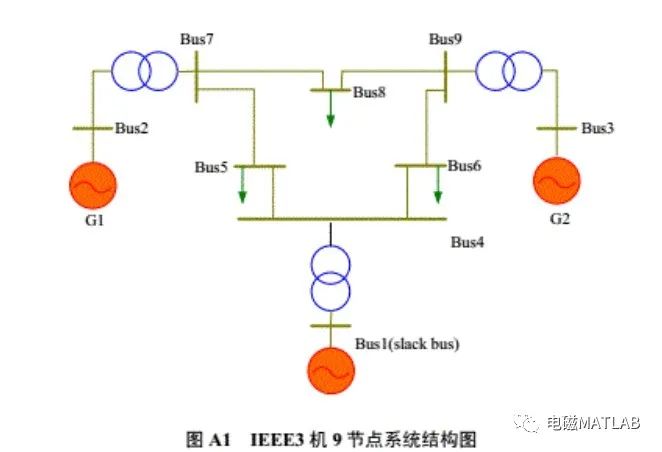
系统结构如下

节点参数如下

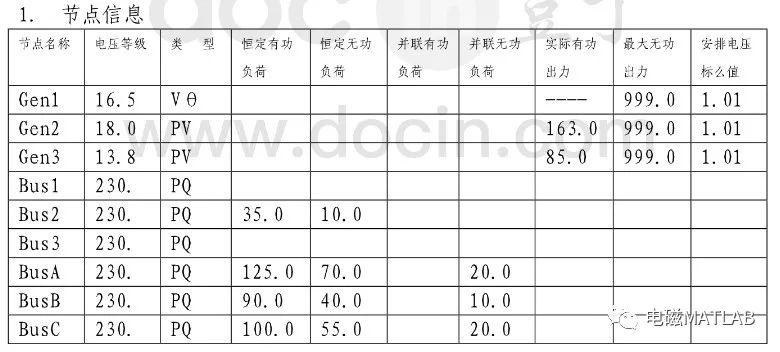
支路参数如下

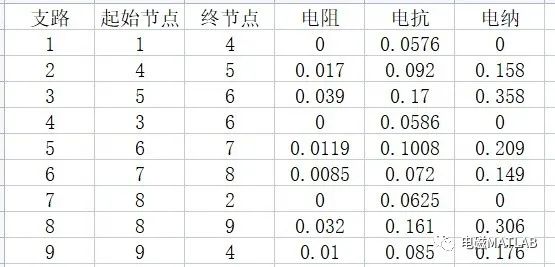
三、matlab程序

1）主函数

clcclose allclear %% 算例mpc = case9;
%% 潮流计算[theta1,P_branch,M,Z,slackbus] = DCpowerflow(mpc);
%% 输出结果disp('=============================');disp('支路潮流矩阵')disp('=============================');disp('')disp([num2str(P_branch)]);


disp('=============================');disp('节点相位矩阵')disp('=============================');disp('')disp([num2str(theta1)]);2）子函数子函数1

function mpc = case9E9    9节点的拓扑情形mpc.version = '2';
%%-----  潮流数据  -----%%%% 基准容量的定义mpc.baseMVA = 100;
%% 节点数据%  bus_i  type  Pd  Qd  Gs  Bs  area  Vm  Va  baseKV  zone  Vmax  Vmin%   其中type为节点类型，pq节点为1,pv节点为2，参考节点为3，孤立节点为4。mpc.bus = [  1  3  0  0  0  0  1  1  0  0  1  1.1  0.9;  2  2  0  0  0  0  1  1  0  0  1  1.1  0.9;  3  2  0  0  0  0  1  1  0  0  1  1.1  0.9;  4  1  0  0  0  0  1  1  0  0  1  1.1  0.9;  5  1  90  30  0  0  1  1  0  0  1  1.1  0.9;  6  1  0  0  0  0  1  1  0  0  1  1.1  0.9;  7  1  100  35  0  0  1  1  0  0  1  1.1  0.9;  8  1  0  0  0  0  1  1  0  0  1  1.1  0.9;  9  1  125  50  0  0  1  1  0  0  1  1.1  0.9;];
%% 电源数据%  bus  Pg  Qg  Qmax  Qmin  Vg  mBase  status  Pmax  Pmin  Pc1  Pc2  Qc1min  Qc1max  Qc2min  Qc2max  ramp_agc  ramp_10  ramp_30  ramp_q  apfmpc.gen = [  1  0  0  0  0  1  0  1  0  0  0  0  0  0  0  0  0  0  0  0  0;  2  163  0  0  0  1  0  1  0  0  0  0  0  0  0  0  0  0  0  0  0;];
%% 支路数据%  fbus  tbus  r  x  b  rateA  rateB  rateC  ratio  angle  status  angmin  angmaxmpc.branch = [  1  4  0  0.0576  0  250  250  250  0  0  1  -360  360;  4  5  0.017  0.092  0.158  250  250  250  0  0  1  -360  360;  5  6  0.039  0.17  0.358  150  150  150  0  0  1  -360  360;  3  6  0  0.0586  0  300  300  300  0  0  1  -360  360;  6  7  0.0119  0.1008  0.209  150  150  150  0  0  1  -360  360;  7  8  0.0085  0.072  0.149  250  250  250  0  0  1  -360  360;  8  2  0  0.0625  0  250  250  250  0  0  1  -360  360;  8  9  0.032  0.161  0.306  250  250  250  0  0  1  -360  360;  9  4  0.01  0.085  0.176  250  250  250  0  0  1  -360  360;];




子函数2

function [theta1,P_branch,M,Z,slackbus] = DCpowerflow(mpc)[n,~] = size(mpc.bus);[L,~] = size(mpc.branch);A = zeros(n);%节点导纳矩阵for i = 1:L    p = mpc.branch(i,1);q = mpc.branch(i,2);    A(p,q) = -1/mpc.branch(i,4);    A(q,p) = A(p,q);endfor i = 1:n    A(i,i) = -sum(A(i,:));endslackbus = find(mpc.bus(:,2)==3);A(slackbus,:) = [];A(:,slackbus) = [];
Z = inv(A);   %%节点阻抗矩阵
P = zeros(n,1);%各个节点的注入功率[x_gen,~] = size(mpc.gen);for i = 1:x_gen    P(mpc.gen(i,1)) = mpc.gen(i,2);endP = P - mpc.bus(:,3);P(slackbus,:) = [];theta = A\P;
index = (1:n)';index(slackbus) = [];theta1 = zeros(n,1);%将平衡点的相角加入，形成所有点的相角矢量[xx,~] = size(index);for i = 1:xx    theta1(index(i)) = theta(i);endtheta1(slackbus) = 0;
P_branch = zeros(L,1);%支路潮流矩阵for i = 1:L    p = mpc.branch(i,1);q = mpc.branch(i,2);    xx = theta1(p) - theta1(q);    P_branch(i) = xx/mpc.branch(i,4);end
M = zeros(n,L);%节点支路关联矩阵for i = 1:L    p = mpc.branch(i,1);q = mpc.branch(i,2);    if theta1(p) > theta1(q)        M(p,i) = 1;M(q,i) = -1;        if p == slackbus            M(p,i) = 0;        elseif q == slackbus            M(q,i) = 0;                end    else        M(p,i) = -1;M(q,i) = 1;        if p == slackbus            M(p,i) = 0;        elseif q == slackbus            M(q,i) = 0;         end    endend