扫码关注
前几天写的关于示波器的文章，提到了探头上面的寄生电容，两个导体并排放置，天然就是一个电容。忽然想到，现如今HDMI 线里面的信号速率到上Ghz，HDMI线也做到了十几米，这么长，等效电容肯定不小啊？这怎么能传呢？信号不都被寄生电容滤波滤没了么?
虽说这个时候也能用均匀传输线理论，集总参数模型，分布参数模型来说一说，但总觉得没理解，如何去想象这个波在里面传输的过程。
我们硬件工程师总能记一大堆的结论，久而久之，总会忘记这些结论是如何推导出来的，甚至忘记了如何通俗的理解这些结论的形成过程。这样造成的后果就是看一些文章都能懂，然而遇到一些新的问题的时候，总不知道如何从理论去分析。
于是乎，我又去翻了翻传输线理论的课本，并用Matlab做了几个实验，感觉挺有意思。
如何理解传输线理论
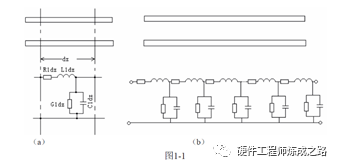
这个推导过程简单概述如下：
首先建立分布参数模型，均匀传输线分割成许多微分段，由电阻，电感，电容，导纳构成，根据基尔霍夫定律，可以列出电流电压的表达式。
然后通过数学微分运算，二阶齐次线性常系数微分方程通解，，最终可推算出传输线上电压和电流表达式：
再根据边界条件，终端电压和电流值，求得一套A1和A2的值（其值为实数常数）。
经过一顿猛于虎的操作之后（作为学渣，能看到这里我还真有点佩服自己了），得出了传输线上各个点的电压公式如下：
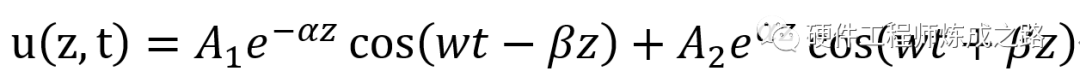
这里z是位置变量，表示到源端的距离，t是时间变量。这个公式的物理意义是什么呢？
第一项指的是信号源向负载方向传播的行波，为入射波，其振幅按照随传输线方向衰减。
第二项指的由负载向信号源方向传播的行波，称为反射波，其振幅按照随传输线反方向衰减。
任一点的波形实际值是入射波和反射波在该点的叠加。
如何理解后面一项是前面一项的反射呢？
从表达式可以看出
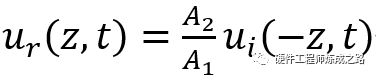
因为A1和A2为实数，所以的波形形状实际是在z处的镜像，只是幅值不同。
我们硬件工程师关注的重点是终端接收到的信号波形，模型如下：
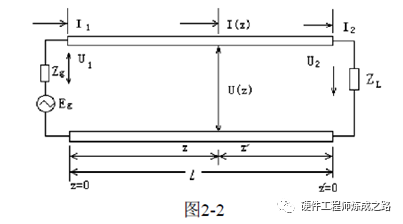
当终端距离源端的距离是n分之一的波长时，相对波长属于短距离传输，可当作无衰减的，因此电压公式变为
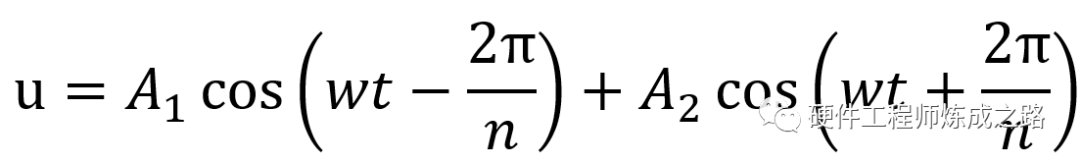
反射系数也可以从推导过程中得出：
反射系数= (ZL-Z0)/ (ZL Z0)
为什么走线短不用用阻抗匹配
经常有个结论，当信号上升沿小于6倍的传输线长度对应的时延，就要看作是高速信号，需要做阻抗匹配了，这个是怎么来的呢？
先来做个试验：
实验目的：看不同反射系数，不同传输线长度，终端波形随实际的变化情况
根据方波的傅里叶傅里叶展开式为
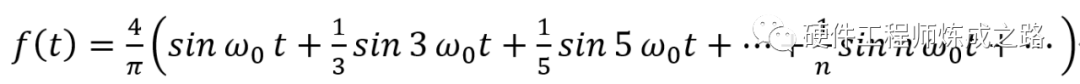
电路中数字信号可以看做是方波，或者是梯形波（取部分谐波）。我们设定一些已知条件来做实验：
---方波频率为w
---传输线长度与基频率波长的比值为length
---终端反射性系数为参量reflex
---源端反射系数为0（为了便于实验，假定源端阻抗匹配好了，不会再发生反射）
原入射波激励函数为：
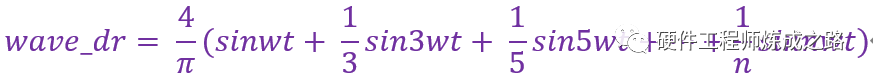
根据这些条件，我们可以求得终端波形函数（入射波和反射波叠加）为：
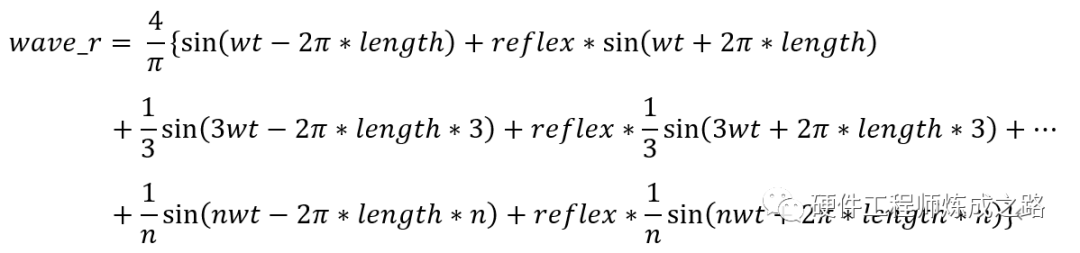
求得源端叠加波形函数为（即我们实际看到的）：
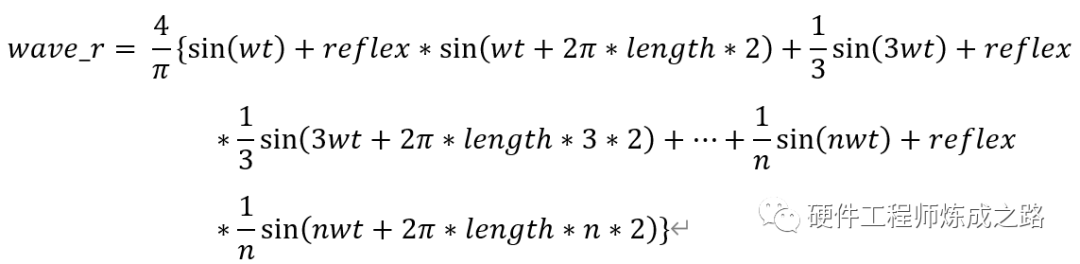
下面来看看图形情况：
1----方波取19次谐波，传输线长度取最高次谐波对应波长的1/3（此时对应信号上升沿等于6倍的传输线延时），终端反射系数为1，波形情况如下
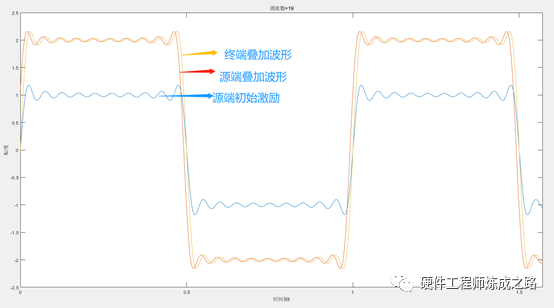
可以看到，基本看不到失真。
这里解释下，为什么源端初始激励是最终看到波形的1一半左右，这是因为终端是全反射的，传输线短，所以入射波和反射波叠到一起就增大了。
另外可能会有疑问，终端波形不是比初始激励大了一倍吗？而现实中我们看到的都是源端和终端一致。这是因为我们实验的前提是源端是阻抗匹配好的，反射系数为0，所以信号经过驱动内阻与阻抗匹配到传输线上，幅度就变成原来一半了，而我们图中的初始激励是已经降低之后的，是在传输线上的。
实际我们测量的源端和终端的波形一致，都是叠加的，从图上也可以看出，源端和终端的叠加波形基本一致，只是有一定的时延。
2----方波取19次谐波，传输线长度取最高次谐波对应波长的2/3倍(此时对应信号上升沿的3倍的传输延时)，终端反射系数为1，波形情况如下
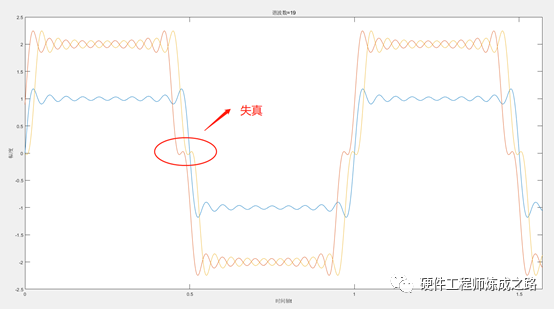
可以看出，波形已经是有明显失真的。
根据前面2个例子，我们就能回答前面提出的问题：信号上升沿小于6倍的传输线长度对应的时延，就要看作是高速信号，需要做阻抗匹配了，这个是怎么来的呢？
好久没用Matlab了，试一下还是挺有意思的，下面贴出源代码，有兴趣的可以自己试验下，可以修改反射系数，传输线长度，谐波数等等，可以看到各种形状，玩一玩能理解更好。
源代码如下:
%方波展开式 wave=4/pi*{sinwt 1/3*sin3wt 1/5*sin5wt ... (1/2n 1)*sin((1/2n 1)wt)}
t=-pi:0.001:5*pi;
omega=2*pi;
reflex=1;%反射系数
n_max = [1:2:1000];
% N=34;0次谐波
N=10;
% for k=1:N
m = 3;%最高波长的m分之1
length = 1/(N*m);
for k=1:N
n=1:2:n_max(k);
b=4./(pi*n);
wave_dr=b*sin(omega*n'*t); %驱动端原始波形
end
for k=1:N
n=1:2:n_max(k);
b=4./(pi*n);
wave_s=b*(sin(omega*n'*t) reflex*sin(omega*n'*t 2*2*pi*length*n')); %源端叠加波形
end
for k=1:N
n=1:2:n_max(k);
b=4./(pi*n);
wave_r=b*(sin(omega*n'*t-2*pi*length*n') reflex*sin(omega*n'*t 2*pi*length*n')); %终端叠加波形
end
figure;
plot(t,wave_dr);%驱动端原始波形
hold on;
plot(t,wave_s);%源端叠加波形
hold on;
plot(t,wave_r);%终端叠加波形
hold off;
% xlabel('时间轴t'),ylabel('幅度')
xlabel('时间轴t'),ylabel('幅度')
axis([0 pi/2 -2.5 2.5])
title(['谐波数=',num2str(n_max(k))])
