滤波器的阶数越高,则可以得到越陡峭的频率响应,使得在通带内尽量不衰减信号,而在阻带内尽可能多地衰减信号。
上一节我们讲的一阶有源滤波器,在对数坐标系上,其阻带内的衰减是20dB/十倍频程;如果想要更好的衰减效果,需要用更高阶的滤波器。
1)二阶有源低通滤波器
一种最简单的二阶滤波器如下图:
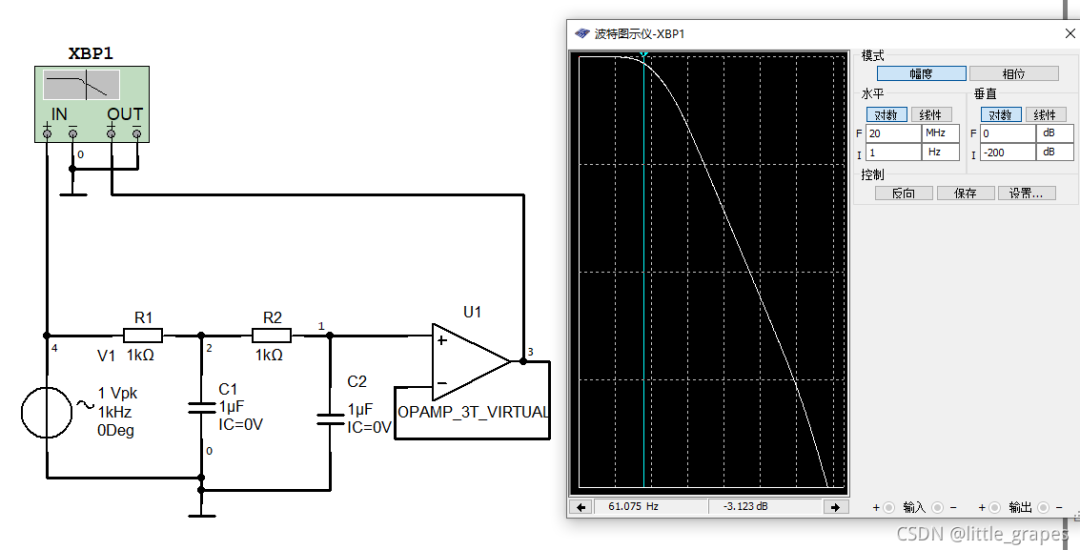
其实质是两个一阶RC滤波器串联之后,再用运放跟随输出,这种滤波器在阻带内的衰减是40dB/十倍频程。
因为是两个RC电路串联,这个电路的传递函数可以简单使用两个RC滤波器的传递函数相乘得到,即:
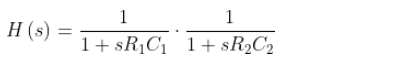
一般情况下,可以取R1=R2,C1=C2,这样便于计算。
当同时需要放大时,可以把运放接成同相放大电路的形式,如下图:
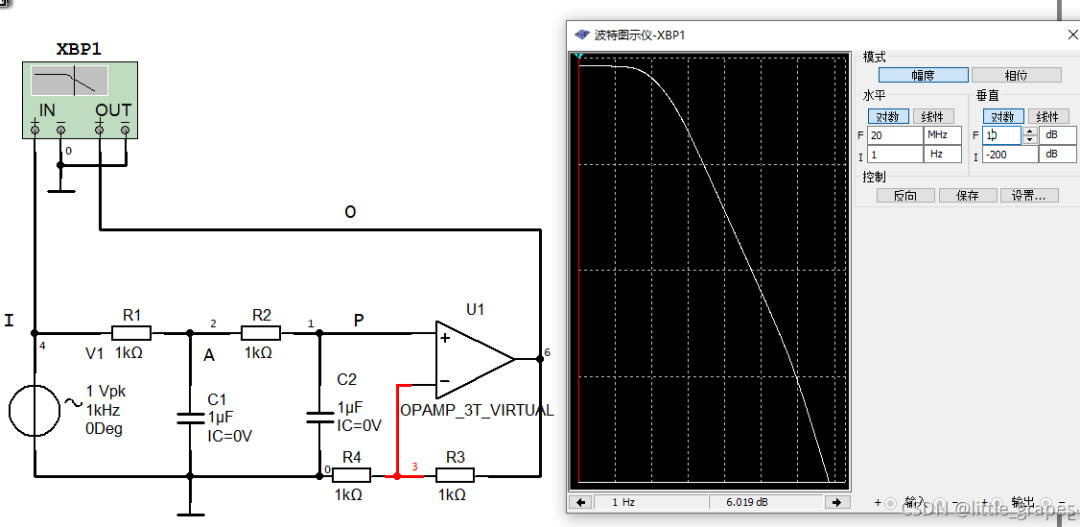
最后一级的同相比例放大电路,可以使得输出放大(R3 R4)/R4倍。
2)另一种二阶有源低通滤波器
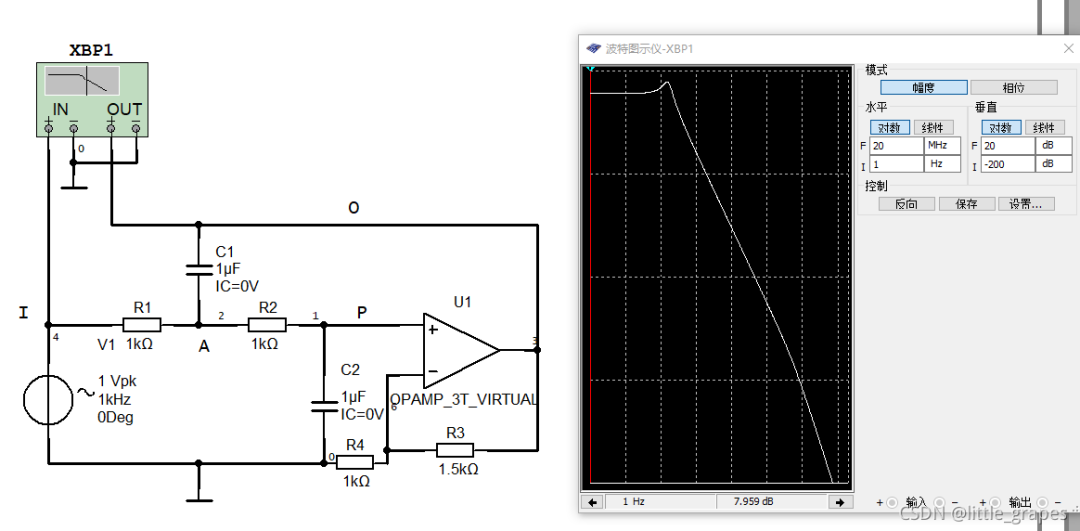
工程中更常见的一种二阶低通滤波器,如下图:

它与1)中的电路不同点在于,第一级的RC的C接到的不是地,而是输出。
我们先计算一下本图中的传递函数,仍然选择R1=R2,C1=C2,并设同相比例放大的倍数(R3 R4)/R4 = Avf;
首先,后一级是个简单的RC滤波器,有:

由于有虚断效应,有:

以A点列电流方程,有:

联立几个式子,可以得到:

可以看到,如果不放大,则结果和1)中电路的传递函数是一样的,但是如果运放有放大倍数,则传递函数不同,大致的图形可以从图中看出区别,1)中电路的增益是单调下降的,而2)在通带和阻带交界出有增益的上升。这个特性使得电路2)有更加分明的通带和阻带分界点。
同时,如果Avf大于等于3,则电路不能稳定工作,会自激震荡。即这个电路不能有太大的放大倍数。
令ωc=1/RC,Q=1/(3-Avf),则传递函数可以化为:
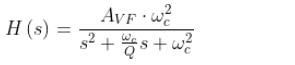
这个式子可以更直观地看出二阶低通滤波器的特性,频率升高时,传递函数以二次方的速率减小。仿真图上可以看出器在阻带内的衰减是40dB/十倍频程减小。
带入的两个参数,ωc为特征角频率,Q为等效品质因数。
3)滤波器设计参数选择
一般情况下,设计滤波器时,先选定电容值(因为常用电容的标称值比电阻少),再由特征频率ωc=1/RC来计算电阻值。
改变放大倍数(即调整Q值),可以发现过渡带的增益凸起有变化,所以如果想要通带内的变化比较平缓,需要调整倍数到合适的Q值。一般Q越大则增益的凸起越明显。

 扫码关注
扫码关注