AC耦合为何必须使用直流均衡信号-凡亿课堂

【摘要】
信号的AC耦合方式具有屏蔽发送端和接收端直流偏置不一致的好处，但并不是所有信号都适合使用这种方式传输，即只有直流平衡信号（数据流中的1与0的数量相等的状态）才可以。本文试图从电容充放电的角度，解释非直流平衡信号不适用于AC耦合方式传输的原因。一、问题的提出在某系统研发过程中，出现了2次串行数据在接收端不能正常接收的情形，均为AC耦合时传输了非直流平衡信号。一次是发送固定码型64个连0然后一个1的变化，在接收端不能正确解码；另外一次为PRBS的数据源经过ADC采样后，每个采样点量化的8bit分别由8个通道传输，每个通道的0,1不均衡，使用AC耦合传输后不能正常接收。为何非直流平衡信号不能通过AC耦合电路，本文试图解释这一问题。二、解决思路1.电容的基本概念电容的定义如公式1所示。Q为电容的电荷量，U为电容两极间电压。根据这个定义可以知道，电容可以储存电荷，储存的电荷量与加在电容上的电压有关。电容在存储或者释放电荷时，必然会有电荷的流动，形成电流。电流的大小如公式2所示。比如电容在充电时，正极板积聚更多正电荷，负极板积聚更多负电荷，电荷的迁徙必将产生电流。这个公式说明，对于同一个电容来说，充放电时电流大小与电容极板间电压的变化快慢有关，变化越快，电流越大。2.电容的充电和放电通俗的解释电容的充电和放电，可以有如下描述。电容充电：两极板的压差变大，积聚更多电荷；电容放电：两极板的压差变小，释放更多电荷；设电容初始电压为V0，最终电压为V∞，则任意时刻t的充电/放电电压为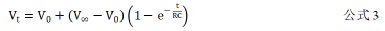

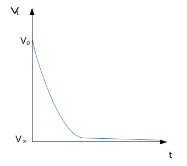
图 1 电容充放电电压曲线一般情况下，在大约3~5RC后，电容的充放电过程就基本完成了。因此时间常数RC直接决定了电容充放电的快慢。根据公式2，对于同一个电路来说（充放电时间一样），充放电前后的压差越大（电容压差定义为|V∞- V0|），那么充放电的电流也就越大。电容的隔直流，通交流特性，也由电容的充放电来解释。如果电容两极的电压不变化，则没有电流和电荷的流动。如果电压发生变化，电路中就会产生电流，电流在电容的另一端就会引起电压的变化。也就是说，直流信号相当于极板间电压无变化，没有电流流过；交流信号，电容在不停的充放电，有电流流过，则相应的电压变化也传递到电容的另外一端。3.电容两端电压不能突变不论电荷聚集到电容极板还是从电容极板释放，都需要一个过程，也就是电容上的电荷值不会突变，根据公式1电容两端的电压也不会突变，而是随着电荷Q的聚集/释放过程而逐渐变化。比如电容两侧目前电压分别为V1=1.2V，V2=0.8V，电容充电完成到达稳态，电容两侧压差为0.4V，左侧极板积聚正电荷，右侧极板积聚负电荷，如图 2所示。

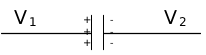
图 2 电容充电稳定图如果电容V1侧电压瞬间增大到1.4V，电容启动充电过程。根据电容两端电压不能突变原理，此时V2处的电压会先升高到1.0V。由于电容为充电过程，V1积聚更多正电荷，V2积聚更多负电荷，释放更多正电荷，致使V2的电压下降，一直到0.8V。这时电容充电过程完成，再次进入平衡状态，此时电容两侧压差达到0.6V。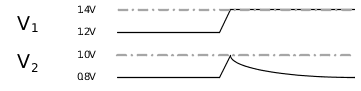

图 3 电容充电时的动态电压变化如果电容V1侧电压瞬间降低到1.0V，电容启动放电过程。根据电容两端电压不能突变原理，此时V2处的电压会先降低到0.6V。由于电容为放电过程，V1释放更多正电荷，V2释放更多负电荷，聚集更多正电荷，致使V2的电压上升，一直到0.8V。这时电容放电过程完成，再次进入平衡状态，此时电容两侧压差达到0.2V。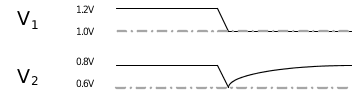

图 4 电容放电时的动态电压变化通过上面的实例分析，可以看到交流信号可以通过电容的原因：如果V1为交流信号，在1.4V和1.0V之间不停的交替变化，那么只要电容充放电的时间足够大，换句话说就是信号周期远小于充放电时间，就可以把这种变化带到V2侧，V2就会在1.0V和0.6V之间不停的交替变化，从而实现了交流信号通过电容。这个在后续章节中有更详尽的分析。本质上，还是由于电路中不停的有电流（电荷的迁徙）流过，最终表现为电压的变化。下面通过对于不同信号的分析，说明交流信号通过电容传输的变化情况。假设一个交流信号V1，经过电容进行AC耦合传输。V1信号的直流偏置为1.2V，摆幅0.4V。经过电容传输后，得到信号V2。V2的直流偏置为V2offset=0.8V。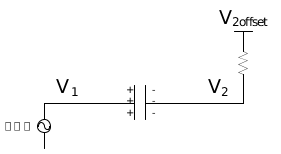

图 5 AC耦合电路示意图4.信号从非直流平衡变为直流平衡V1从常低变为交流

图6 从常低电平到平衡信号的转换 t1时刻：V0=1.0-0.8=0.2，V∞=1.4-0.8=0.6，电容压差变化|V∞-V0|=0.4V。到达t2时，电容完成了时间为∆t的充电过程，由于充电导致的V2电压变化∆V，即t2时刻V2=1.2-∆V。t2时刻：V0=1.4-（1.2-∆V）=0.2 ∆V，V∞=1.0-0.8=0.2，电容压差变化|V∞-V0|=∆V。到达t3时，电容完成相同时间∆t的放电过程，由于放电导致的V2电压变化∆V’，到t3时刻V2=0.8-∆V ∆V’。结合第2小节中电容充放电时间的解释，对于同一个电路，电容压差变化（|V∞-V0|）越大，充放电的时间越短，或者说相同的时间内电容压差变化（|V∞-V0|）越大，极板电压变化（V2）越大。结合本例，在第一个∆t间隔内，电容压差变化0.4V，而第二个∆t间隔内电容压差变化∆V，0.4>>∆V，因此在相同的时间间隔∆t内，∆V大于∆V’，也就是说充电量大于放电量。这就解释了中的V2曲线的平均值不断下降的原因。V1从常高变为交流

图 7 从常高电平到平衡信号的转换 t1时刻：V0=1.4-0.8=0.6，V∞=1.0-0.8=0.2，电容压差变化|V∞-V0|=0.4V。到达t2时，电容完成了时间为∆t的放电过程，由于放电导致的V2电压变化∆V，即t2时刻V2=0.4 ∆V。t2时刻：V0=1.0-（0.4 ∆V）=0.6-∆V，V∞=1.4-0.8=0.6，电容压差变化|V∞-V0|=∆V。到达t3时，电容完成相同时间∆t的充电过程，由于充电导致的V2电压变化∆V’，到t3时刻V2=0.8 ∆V-∆V’。结合第2小节中电容充放电时间的解释，对于同一个电路，电容压差变化（|V∞-V0|）越大，充放电的时间越短，或者说相同的时间内电容压差变化（|V∞-V0|）越大,极板电压变化（V2）越大。结合本例，在第一个∆t间隔内，电容压差将变化0.4V，而第二个∆t间隔内电容压差变化∆V，前者电容压差变化远大于后者，因此在相同的时间间隔∆t内，∆V大于∆V’，也就是说放电量大于充电量。这就解释了中的V2曲线的平均值不断上升的原因。5.信号为稳定的直流平衡第4小节中的信号，经过长时间的变化，总会有一个时刻在一个∆t间隔内的充电量与放电量达到平衡，如图 8所示。

图 8 AC耦合传输直流平衡信号波形图t1时刻，由于前一个时间间隔内电容放电，V2=0.6 ∆V，则V0=1.0-（0.6 ∆V）=0.4-∆V，V∞=1.4-0.8=0.6，电容压差变化|V∞-V0|=0.2V ∆V。到达t2时，电容完成了时间为∆t的充电过程，由于充电导致的V2变化为∆V’，则在t2时刻V2=1.0V ∆V-∆V’。T2时刻：V0=1.4-（1.0V ∆V-∆V’），V∞=1.0-0.8=0.2V，电容压差变化|V∞-V0|=0.2-∆V ∆V’，到达t3时，电容完成了时间为∆t的放电过程，由于放电导致的V2变化为∆V’（充电和放电达到平衡，在相同时间内电压变化也相同），则在t3时刻V2=1.0-V0=0.6 ∆V-∆V’ ∆V’=0.6 ∆V。由于充电和放电达到平衡，因此在t1和t2时刻计算的电容压差变化应该相等，即0.2V ∆V=0.2-∆V ∆V’，即∆V’=2∆V。如果放大这个时间片段的话（夸张的画），应该如图 9所示。也就是说，在V1的每次升高或者降低变化时，电容都在进行充电或者放电过程，只不过充放电的时间与信号变化的时间比拟起来很长，以至于几乎看不到充放电对V2信号电平的影响。

图 9 AC耦合直流平衡信号局部放大6.信号从直流平衡变为非直流平衡V1从交流变为常低。根据前两节的分析，一旦V1变为低电平，电容就会开始放电，由于V1没有再变高的过程，放电会一直持续，一直到电容重新达到平衡状态，也就是电容压差最终稳定在0.2V。

图 10 V1变为常低后V2的变化图V1从交流变为常高。根据前两节的分析，一旦V1变为高电平，电容就会开始充电，由于V1没有再变低的过程，充电会一直持续，一直到电容重新达到平衡状态，也就是电容压差最终稳定在0.6V。

图 11 V1变为常高后V2的变化图7.单端信号到差分信号事实上，经常使用AC耦合的情形多为差分信号传输，那是由于不同标准电平的差分信号直流偏置会有差别，通常需要使用AC耦合进行直流偏置的隔离。对于差分信号，如果发送端直流不平衡时，在接收端又会是什么现象呢？根据前面各小节的分析，得到差分信号的传输波形就是很简单的了。章节4和章节6中均分析了两种数据的波形，将这两种数据分别定义为VP和VN，那么两者相减就得到差分信号的波形了，分别如图 12和图 13所示。仅从波形上看，与单端信号差别不大，仅信号的摆幅比单端信号大了一倍而已。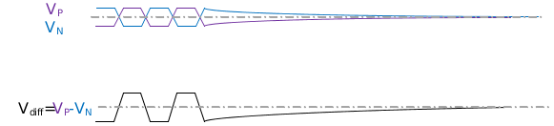

图 12 差分信号从交变电平到常电平

图 13 差分信号从常电平到交变电平8.信号非直流平衡时的问题综合上面的分析，如果信号出现非直流平衡，即常连0或者常连1的数量过多时，可能会造成两个方面的问题：

（1）超过信号的判决门限而造成误判任何信号在接收端都会有一个判决门限，比如LVDS信号会有±100mV的门限要求，即Vdiff落在0±100mV内，接收端无法判断接收数据位逻辑0还是逻辑1，可能造成误判。从图 12可以看出，如果发送端出现常连0或者常连1时，电容会过度充电或者过度放电，使接收端的电压可能降低到判决门限（比如LVDS信号的±100mV）以内，造成误判；从图 13可以看出，发送端在常连0或者常连1后，如果出现变化bit，最开始的几个周期这些信号在接收端有摆幅很小的时刻，如果同样落在判决门限（比如LVDS信号的±100mV）以内，也会造成误判。

（2）超过器件能承受的最大电压损坏器件从章节4可以看出，V1在常连0或者常连1后出现一个变化bit，V2会出现较大的上摆或者下摆（会到达1.2V或者0.4V），有可能会超过接收器件承受的最大电压，造成器件的损害。基于上述两个问题的分析，得到AC耦合电路需要使用直流平衡的信号。当然直流平衡并不是要求信号如前面章节分析的0和1交替反转的那样，本文中使用这样的信号仅为分析方便。实际使用中只要0和1的数量相等或者近似相等就可以了，出现连续的0或者连续的1不可避免，但只要不太多就可以了。比如8B/10B编码，连续的“1”或“0”不超过5位，即每5个连续的“1”或“0”后必须插入一位“0”或“1”。三、实践情况针对上述的理论分析，进行相应仿真。为了能够更好的理解数字序列经过AC耦合通路后的波形，首先仿真脉冲信号经过电容后的波形变化，1.脉冲信号根据图 5建立如图 14所示仿真模型，信号源为阶跃函数，上升沿1ps，摆幅0.2V，经过一个电容得到信号out1。由于电容电压的不可突变特性，在信号源in1的阶跃过程中都会出现out1电压先上升后下降到0.8V的过程，但如果电容值选择不同，out1的变化速度也不同。下面仿真了三种不同电容值时阶跃响应曲线。

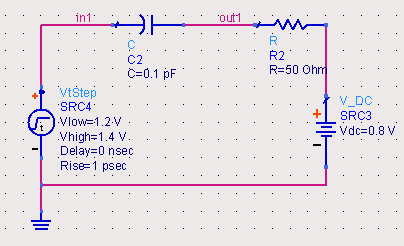
图 14 阶跃仿真模型1.1充电时间短（15ps）选择电容C=0.1pF，计算电容的充电时间约为3RC=15ps，而信号的上升沿为1ps，这两个时间相差不多。根据仿真波形图 15所示，由于充电时间很短，导致out1的电平在瞬间没有上升到1.0V。

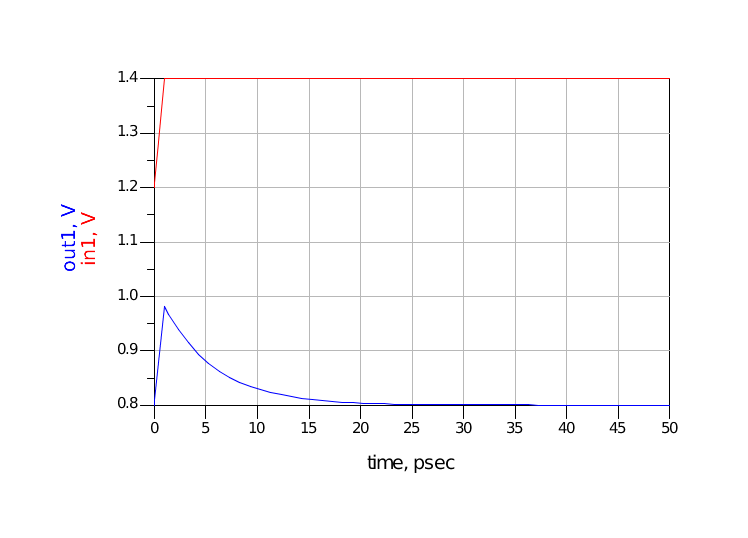
图 15 C=0.1pF仿真波形1.2充电时间中等（15ns）选择电容C为0.1nF，此时电容的充电时间约为3RC=15ns。而信号的上升沿为1ps，相差不多。在阶跃信号开始时，out1可以到达1.0V，并且在维持较短的一段时间开始下降，仿真波形分别如图 16和图 17所示。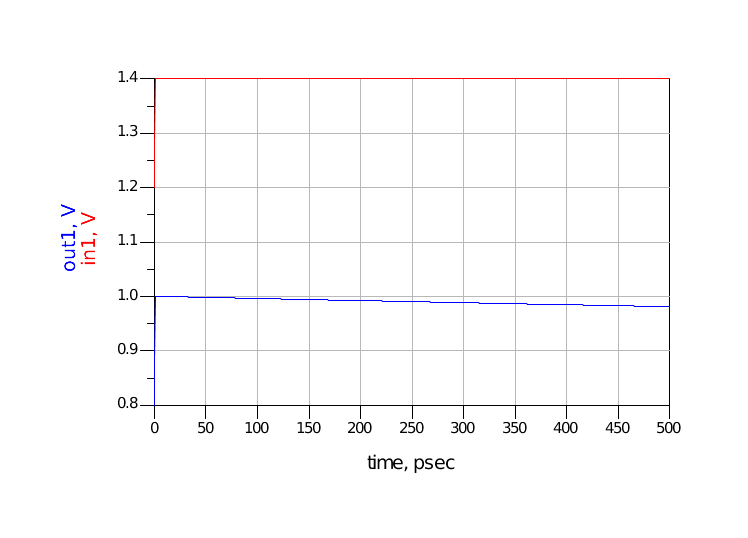

图 16 C=0.1nF仿真波形（仿真时间500ps）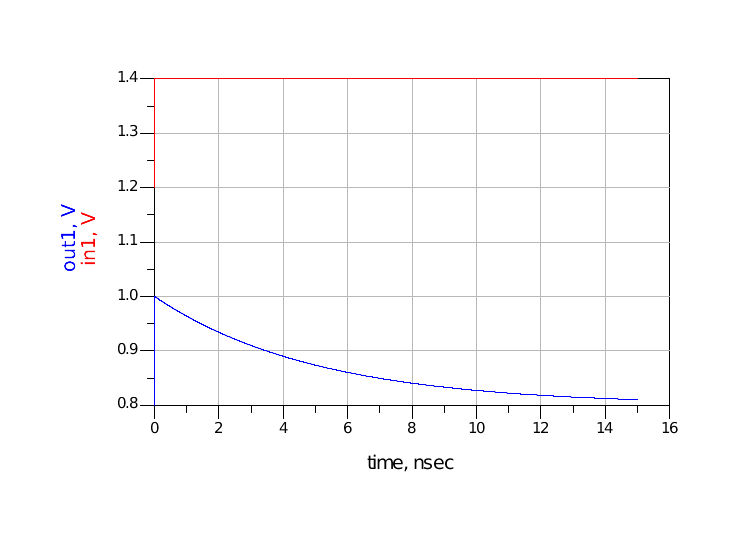

图 17 C=0.1nF仿真波形（仿真时间15ns）1.3充电时间长（15us）选择电容C为0.1uF，此时电容的充电时间约为3RC=15us，而信号的上升沿为1ps，相差非常大。由于充电时间过长，在很长一段时间内（比如15ns内）out1没有明显变化，仿真波形分别如图 18和图 19所示。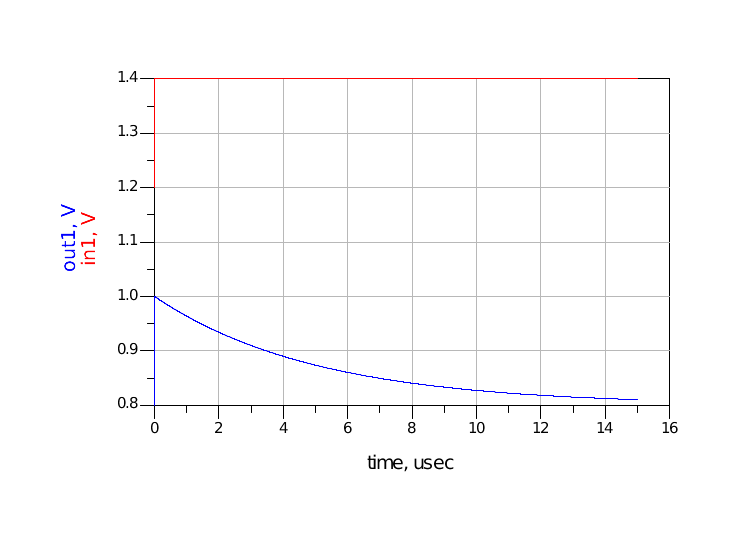

图 18 C=0.1uF仿真波形（仿真时间15us）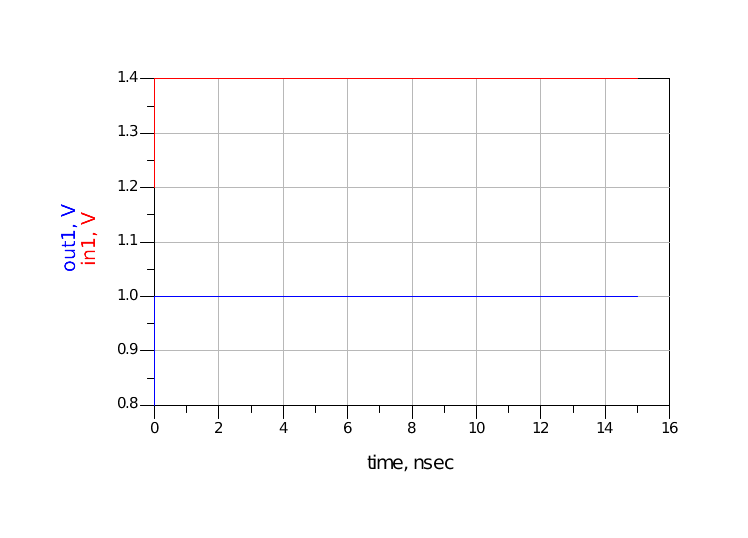

图 19 C=0.1uF仿真波形（仿真时间15ns）2.DC平衡数字序列将仿真模型的信号源更换为DC平衡的bit序列，序列频率为2620MHz（周期380ps），摆幅0.4V，直流偏置1.2V，同样针对三种电容值进行仿真。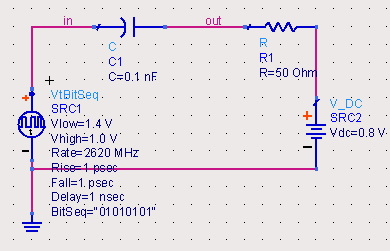

图 20 DC平衡数据源仿真模型2.1充放电时间短仿真模型的电容C为0.1pF，充放电时间15ps。而bit序列的周期为380ps，半个周期为190ps，也就是说在信号的半个周期内，电容很快完成了充电/放电过程，out波形不能维持在固定的高电平或者低电平。最终仿真波形如图 21所示，这个电容值不适合DC平衡信号的传输。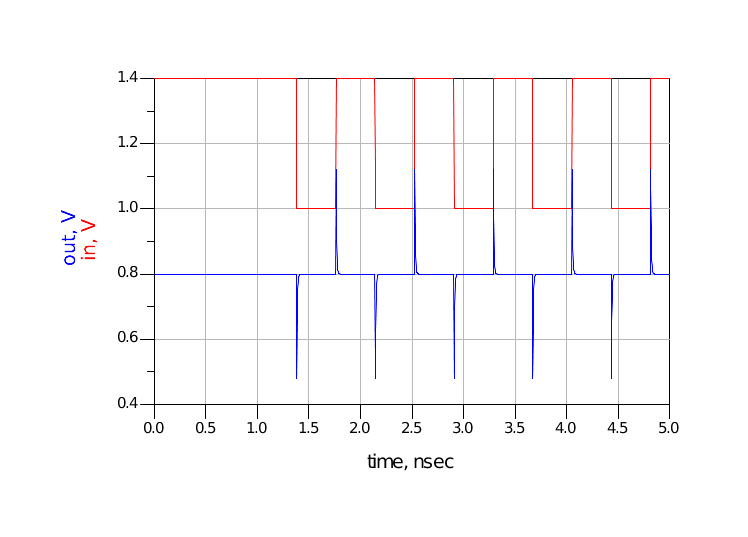

图 21 C=0.1pF仿真波形2.2充放电时间中等仿真模型的电容C为0.1nF，充放电时间15ns。而bit序列半个周期为190ps，这个时间差距中等，最终仿真波形如图 22所示。out波形到达正常（直流偏置为0.8V）大约花了15ns的时间。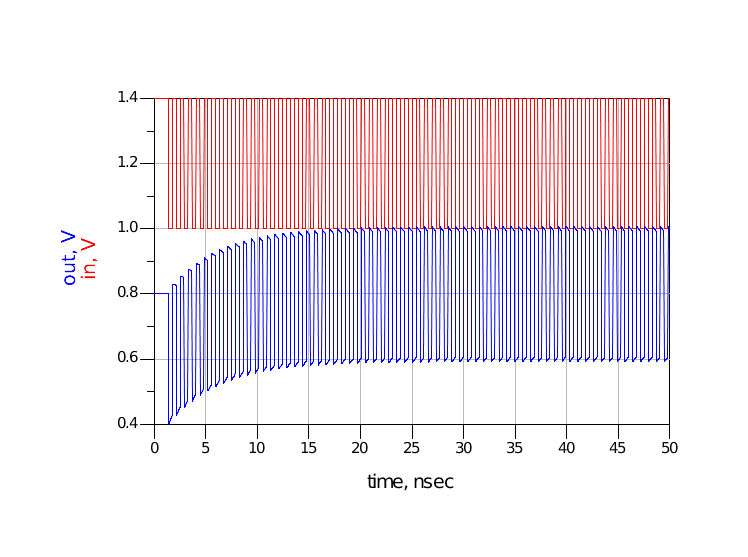

图 22 C=0.1nF仿真波形2.3充放电时间长仿真模型的电容C为0.1uF，充放电时间15us。而bit序列半个周期为190ps，这个时间差距还是非常大的，也就是说在信号半个周期内，电容充电/放电过程进行的非常缓慢，最终仿真波形如图 23所示。out波形到达正常（直流偏置为0.8V）大约花了15us的时间，在这三种情形中是最长的一个。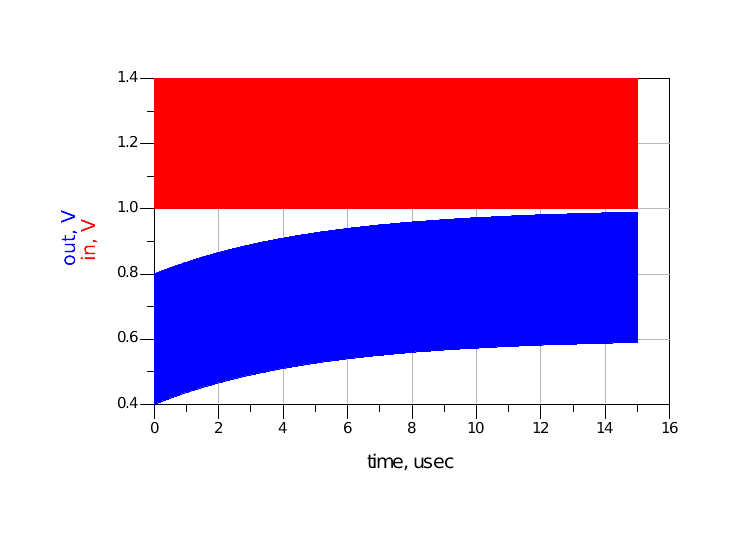

图 23 C=0.1uF仿真波形3.DC非平衡数字序列仍然使用上一节中的仿真模型，将发送bit序列更改为“11111111111111111111111111111111111111111111111111111111111111110”形式的非DC平衡序列，电容选择0.1nF。由于“0”的数量较少，导致电容放电时间短，形成图 24所示的波形，与第二章中的分析一致。这种信号在接收端就可能造成器件损坏或者接收判决错误。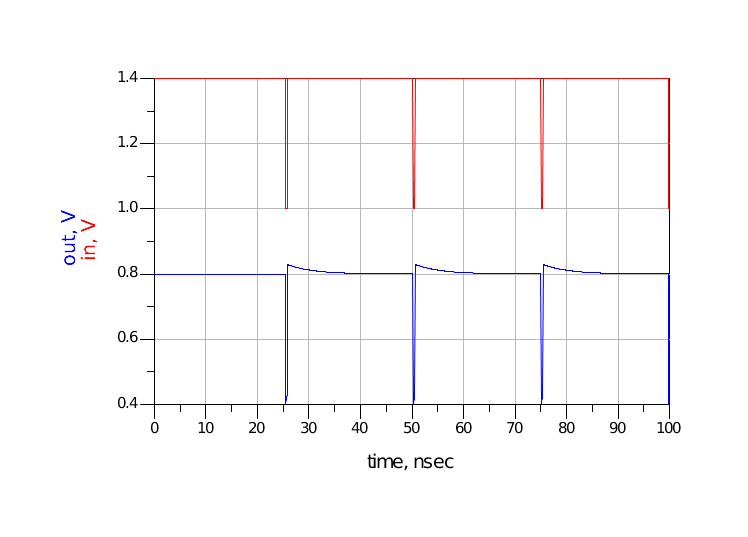

图 24 非DC平衡信号仿真波形a将发送bit序列更改为“11111111111111111111111111111111111111111111111111111111111111110101010101010101010101”形式的非DC平衡序列，电容仍选择0.1nF，out的波形如图 25所示。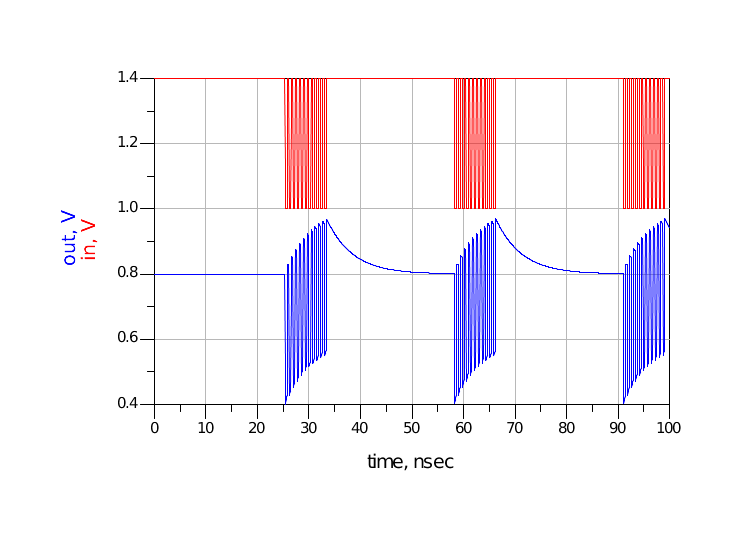

图 25 非DC平衡信号仿真波形b四、总结通过本文的分析和仿真，从电容充放电的角度，比较直观的解释了非DC平衡信号不能使用AC耦合传输的原因。同时在分析过程中，我们可以得到以下进一步引申的结论：1.隔直电容的选择与信号频率有关。如果信号的频率较低，隔直电容不能选择的太小（充放电时间太小），以防止出现图 15所示的情形，使传输波形失真；2.非DC平衡信号，经过AC耦合传输，信号眼图一般不会闭合，但眼图的中心电平会有偏移，眼皮变厚，眼高也会变小。结论1根据上述章节的分析以及仿真波形显而易见；结论2进一步阐述如下：结合第二章中的分析以及图 24和图 25的仿真波形，可以看到AC耦合后的信号会经历一个摆动调整的过程，从最原始的波形向偏置为0.8V调整。如果信号一直在这个区间内调整，那么输出信号眼图将如图 26所示，其中红框为非DC平衡信号经过AC耦合后的眼图（最坏情况），蓝色为DC平衡信号经过AC耦合后的眼图（眼高为摆幅，眼中心为直流偏置Voffset）。如果信号源为图 24使用的源，那么AC耦合后的眼图与图 26中的黑色框类似，眼图中心会达到VL；如果信号源为图 25使用的源，那么AC耦合后的眼图将介于黑框和红框之间。