「电池组」的连接与可靠性

一、动力电池单体内各组件的逻辑关系

动力电池单体是由正极群、负极群、多孔性隔膜、外壳、电解液、排气阀6个主要组件组成的，其中任何一个组件出了故障都会给动力电池单体的可靠性带来损害，即降低了整只动力电池单体的可靠度R（t）。因而从逻辑关系上来分析，动力电池单体的这6个主要组件的关系应当是串联的，那么整个动力电池单体的可靠度R（t）将由各个组件的可靠度Ri（t）(1·2……i)来决定。

动力电池单体的正极群和负极群又都是分别由许多片正极板和负极板组成的，从电气连接上来看，各片正（或负）极板都是并联在一起的；从逻辑功能方面看，任何一片极板的失效并不会导致整只动力电池单体失效，必须全部极板同时失效才会引起极群失效，因而它们也可视为并联的。

二、动力电池单体的可靠性模型

动力电池单体的可靠性模型，大体上有以下三种形式：

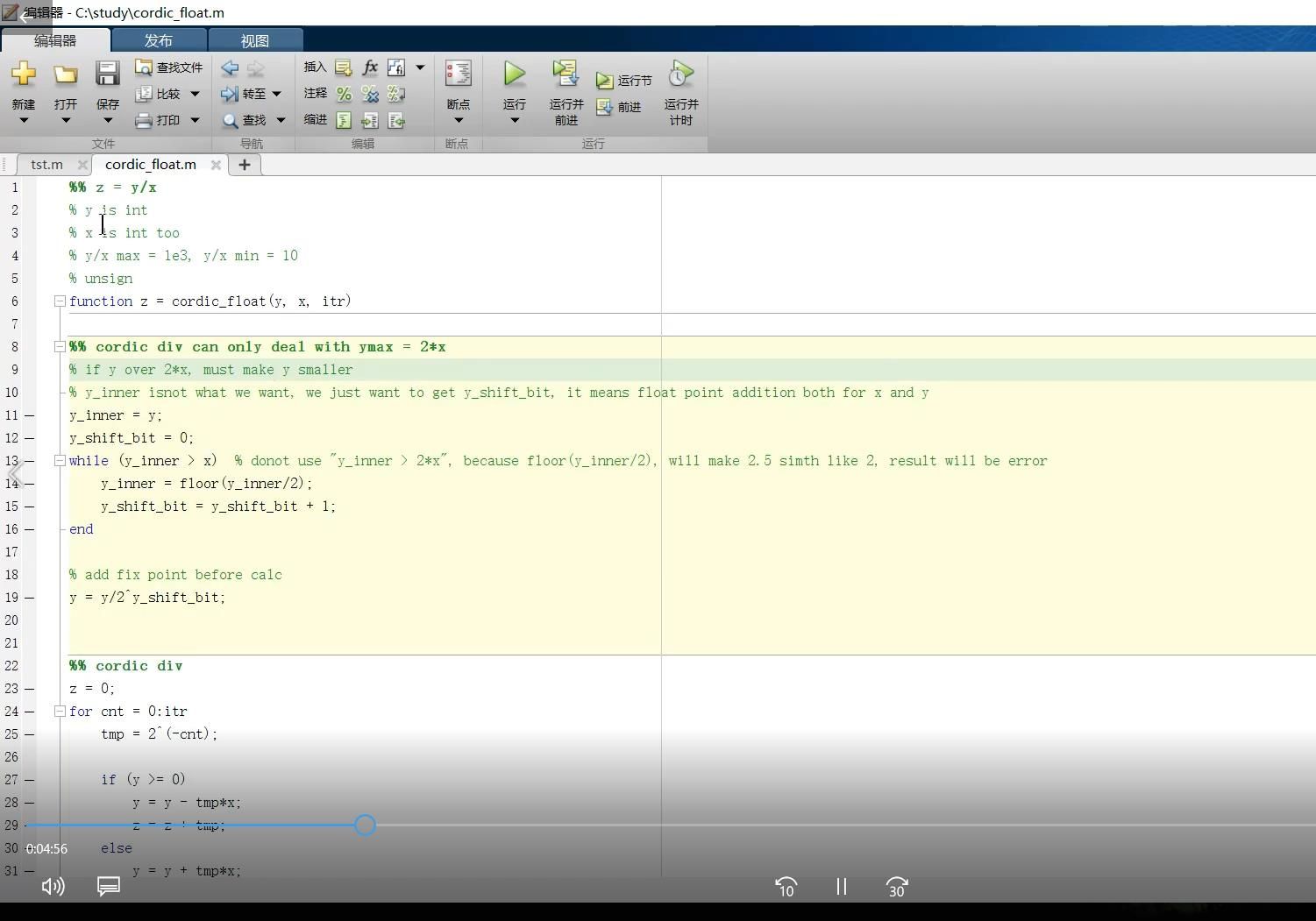
（1）首先是串联系统的可靠性模型：串联系统模型如图1所示。串联系统是指它的每一个元件对于系统的正常工作都是必须的，不可或缺的；任何一个元件的失效，将导致系统工作不正常。这是一种较常见和简单的系统。

如果系统有N种元件，每种元件的失效率为λi(i=1～N)，则：

串联系统的总失效率：λΣ=n1λ1＋n2λ2＋……nNλN；

总的无故障工作时间：MTBFΣ=1/λΣ=1/[n1λ1＋n2λ2＋……nNλN]；

年可靠度：P=1/e8760·λΣ=1/e8760/MTBFN(因为每年时间共8760h)。

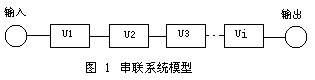
（2）并联系统的可靠性模型：并联系统模型如图2所示。图2中U1，U2均可单独地实现系统的功能，而且U1，U2任何一个单元出现故障，将自动（或手动）和输入、输出端断开，同时接入另一个互为备份的单元。显然并联系统的任何一个单元的失效，均不会影响系统的功能，只有在二个单元均失效时，系统才不能正常工作。同理也可以N个单元并联构成一个系统。

其数学关系为：

故障概率：F（t）=F1（t）·F2（t）…FN（t）；

若F1（t）=F2（t）…=FN（t）则可靠度：R（t）=1－F（t）=1－[F1（t）]n。

结论很明确，在每个单元的可靠性受各种限制不可能太高，而又要求系统具有很高的可靠度的情况下，采用并联系统代替串联系统是提高电子系统可靠性的根本方法。并联系统的成本将高于串联系统，但为了保证必要的可靠性，花些代价是必须的也是值得的。

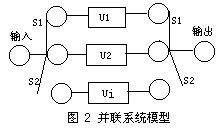
（3）混合系统可靠性模型

实际工程中，为了在成本和可靠性方面求得平衡，常常使用串联和并联混合系统。也就是对可靠度较低的单元采用并联系统，可靠度高的单元保持串联系统。模型如图3所示。

混合系统的可靠度：R（t）=R1（t）·R2（t）·R3－2（t）·R4（t）；

如果R1=R2=R4=0.99，R3=0.9，则R3－2=1－[1－R3]2，R3－2=0.99，R=R1·R2·R3－2·R4=0.96=96％（F=4％）。

假使，U3不用并联系统，则R=0.87=87％，（F=13％）。

可见，两者可靠度的差别还是很明显的，故障率降低了3倍多。总的来说，混合系统比串联系统可靠性高，比并联系统简单。

三、动力电池组

动力电池组是指动力电池单体经由串并联方式组合并加保护线路板及外壳后，能够直接提供电能的组合体，动力电池组是组成动力电池系统的次级结构之一。动力电池模组是由多个单体电芯串并联组装而成，单体电芯之间连接与紧固，要求连接片与电池的极柱接触电阻小、抗振动、牢靠程度高。

无论是用激光焊焊接、电阻焊焊接还是螺栓机械锁紧，都必须保证成组后的电池系统在电动车辆实际行驶过程中的可靠性和耐久度。在不同的动力电池系统设计需求里，其体积能量密度、质量比能量密度以及体积功率密度等都会与动力电池系统中单体电池之间连接结构与工艺相关。

按动力电池组电芯的结构形状来分，主要分为圆柱电芯和方形电芯，各自的优缺点也十分明显，从外壳材质上可分为金属壳（钢壳或铝壳）和铝塑膜封装（聚合物锂电池）。从极柱类型上又可以分为外螺纹极柱、内螺纹型极柱、平台型极柱以及铝镍长条型极耳（聚合物锂电池类型的极耳）。

不同极柱类型的电池，在电池成组方式、连接工艺也会有很大不同，同时有各自的优缺点。动力电池模组是由多个单体电池连接组成，而单体电池之间连接的方法和工艺的选择需根据电池类型及其极柱（极耳）的类型来定。在一定程度上，电芯的性能决定了电池组的性能进而影响整个动力电池系统的性能。

因此在进行动力电池系统设计，一定要根据整车的设计要求去选择电芯的材料及形状。

四、动力电池组连接与可靠性

在采用动力电池单体构成动力电池组时，常采用以下两种连接方式：

①将动力电池单体先串联后在并联的组合方式；

①将动力电池单体先并联后在串联的组合方式。

（1）先串联后在并联组合方式的可靠性

将动力电池单体先串联后在并联的组合方式可用来提高供电系统的可靠性，是当动力电池单体先串联后已不能保证用户提出的可靠性要求时，就可以再并联一组同规格的动力电池单体来提高可靠性。为了有一个量的概念，图4给出了先串联后在并联的组合方式的可靠性模型图：

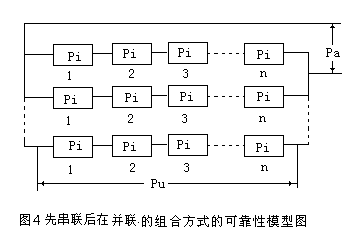
假定各动力电池单体的可靠度相同Pi=0.99，则图4中PU是动力电池单体的可靠性，这两部分是串并联冗余的关系。

那么根据可靠性并联的计算公式，动力电池单体的可靠性PU是：

PU＝Pi/n（n为动力电池单体的个数）。

动力电池单体串联后在并联的组合方式的系统可靠性Pa是：Pa＝1-（1-PU）（1-PU）×……×（1-PU）。

由上面的结果可以看出，两个可靠性都为0.99的单元并联后，其可靠性增加到100倍，不可靠性由百分之一下降到万分之一。

（2）先并联后在串联组合方式的可靠性

将动力电池单体先并联后在串联的组合方式可用来提高供电系统的可靠性，是当动力电池单体先串联后已不能保证用户提出的可靠性要求时，就可以再将同规格的单动力电池单体并联后在串联来提高可靠性。为了有一个量的概念，图5给出了先并联后在串联的组合方式的可靠性模型图。

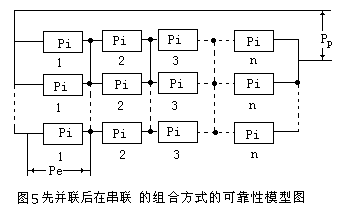
如果假定动力电池单体的可靠度为Pi=0.99，则图5中Pe是动力电池单体的可靠性，这两部分是并联冗余的关系。

那么根据可靠性并联的计算公式，动力电池单体的可靠性PU就是：Pe＝nPi；

动力电池单体串联后在并联的组合方式的系统可靠性Pp是：Pp＝1-（1-Pe）（1-Pe）×……×（1-Pe）。

由上面的计算公式可以从理论上定性和定量地看出可靠性的趋势是：PP＞Pi。

显然，采用先并联后串联的方式组成的动力电池组，其可靠度将比先串联后并联的方式要高。如果考虑到动力电池单体的不均匀性，那么这种先并联后在串联的连接方式对防止出现两组动力电池组偏流有利。