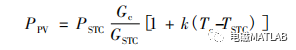模糊控制算法实例matlab程序

以水位的模糊控制为例。如图4一4所示，设有一个水箱，通过调节阀可向内注水和向外抽水。设计一个模糊控制器，通过调节阀门将水位稳定在固定点附近。按照日常的操作经验，可以得到基本的控制规则为：“若水位高于0点，则向外排水，差值越大，排水越快”；“若水位低于0点，则向内注水，差值越大，注水越快”。

根据上述经验，可按下列步骤设计一维模糊控制器。

1 确定观测量和控制量

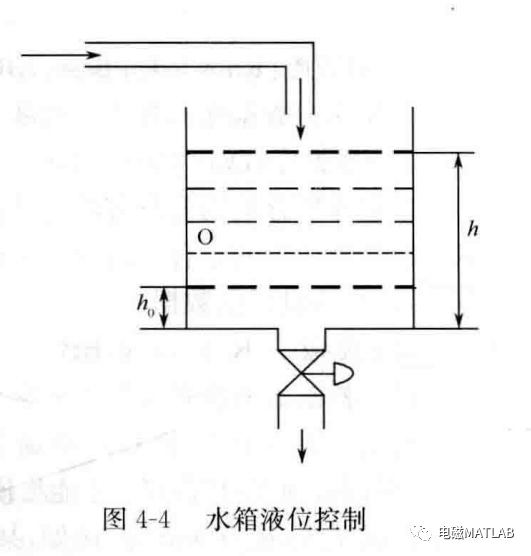
定义理想液位0点的水位为h0，实际测得的水位高度为h，选择液位差为

将当前水位对于h0点的偏差e作为观测量。

2 输入量和输出量的模糊化

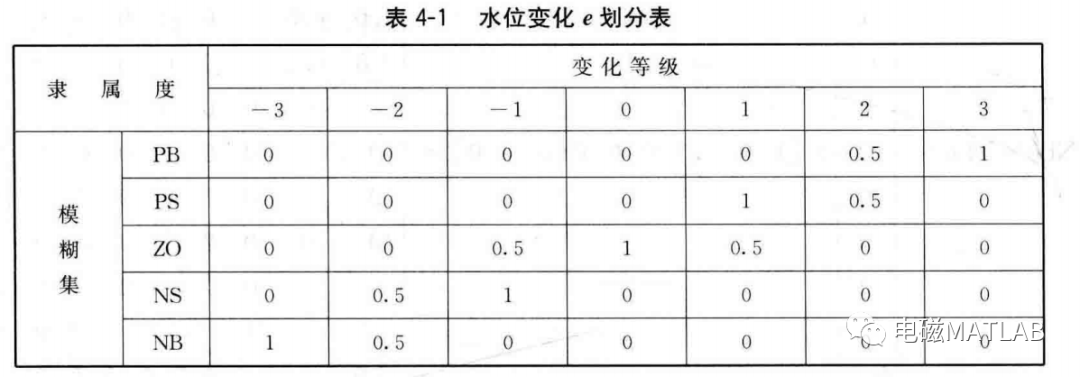
将偏差分为5个模糊集：负大（NB），负小（NS），零(ZO)，正小（PS），正大(PB)。将偏差e的变化分为7个等级，-3，-2，-1，0， 1， 2， 3，从而得到水位变化模糊表，见表4一1。

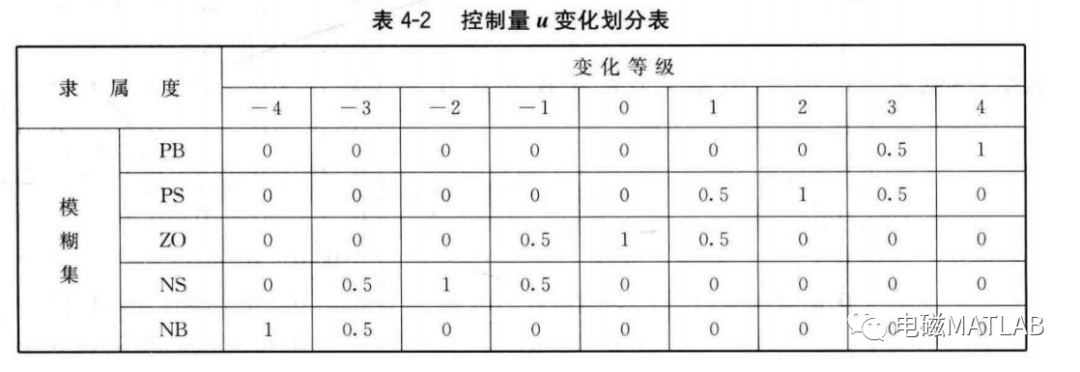
控制量为调节阀门开度的变化。将其分为5个模糊集：负大(NB)，负小（NS），零（ZO），正小(PS)，正大(PB)。将的变化分为9个等级：一4，一1，0， 1， 2， 3， 4，得到控制量模糊划分表，见表4一2。

3 模糊规则的描述

根据日常的经验，设计以下模糊规则：

(1)"若负大，则负大”；

（2）“若e负小，则负小”；

（3）“若e为零，则为零”；

（4）“若e正小，则正小”

（5）“若e正大，则正大”

其中，排水时为负，注水时为正。

将上述规则采用“'IF A THEN B”的形式来描述，则模糊规范表示为

(l)if e = NB Then u =NB

(2)if e = NS Then u =NS

(3)if e = ZO Then u =ZO

(4)if e = PS Then u =PS

(5)if e = PB Then u = PB

根据上述经验规则，可得模糊控制规则表，见表4一3。

4 求模糊关系

模糊控制规则是一个多条语句，它可以表示为U×V上的模糊子集，即模糊关系R为

R=(NBe×NBu)U(NSe×NSu)U(ZOe×ZOu)U(PSe×PSu)U(PBe×PBu)。其中规则内的模糊集运算取交集，规则间的模糊集运算取并集，即

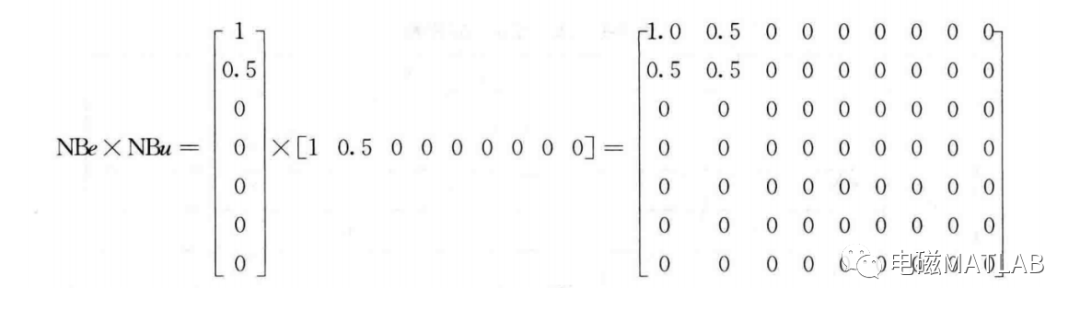
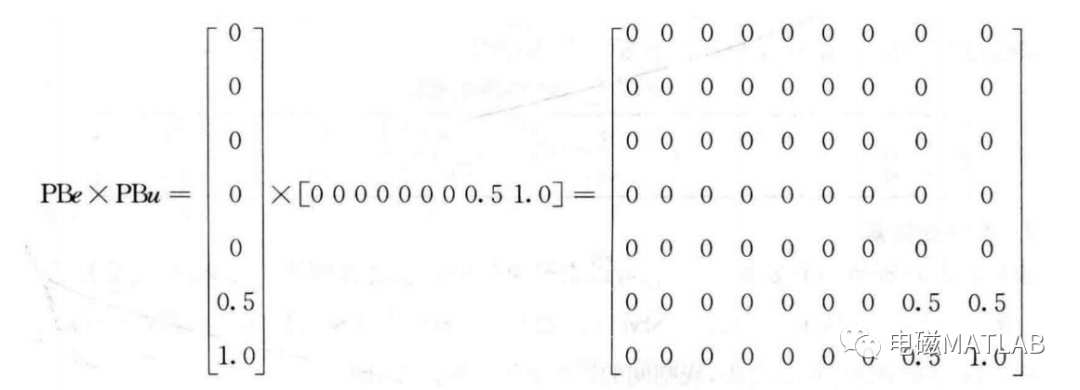
由以上可得：

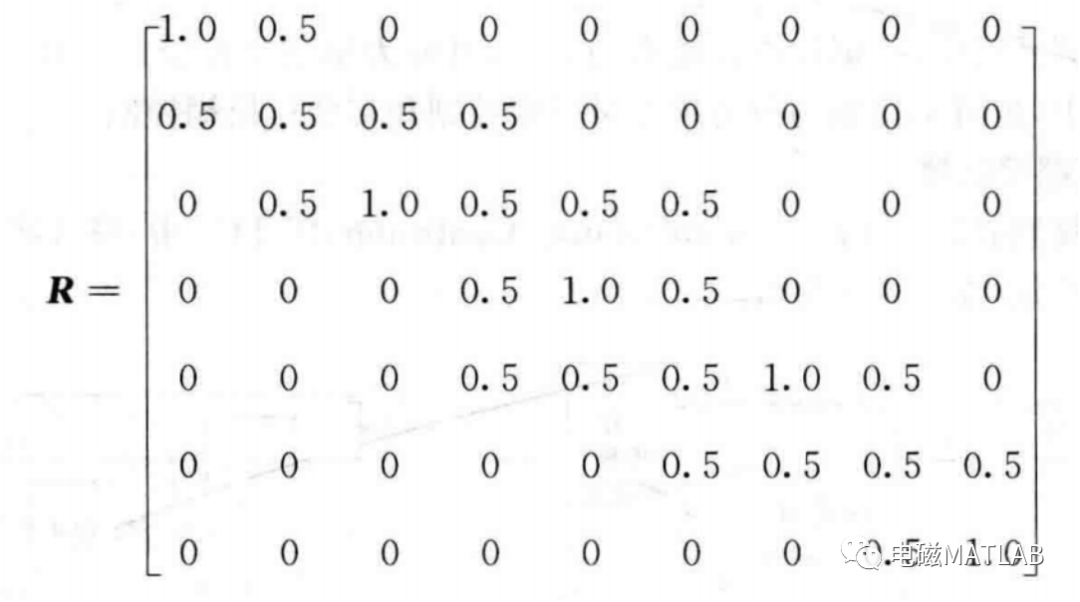
5  模糊决策

模糊控制器的输出为误差向量和模糊关系的合成，即

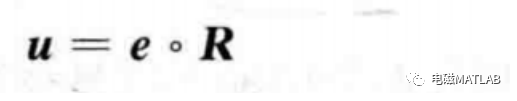
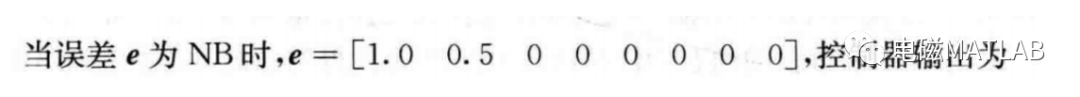
6 控制量的反模糊化

由模糊决策可知，当误差为负大时，实际液位远高于理想液位，e=NB，控制器的输出为一模糊向量，可表示为

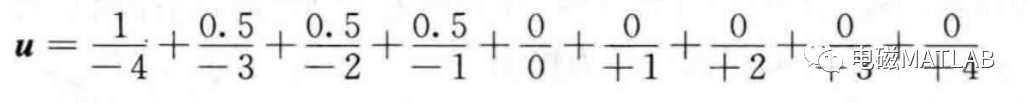
如果按照“隶属度最大原则”进行反模糊化，选择控制量为u=-4，即阀门的开度应开大一些，加大排水量。如下图：

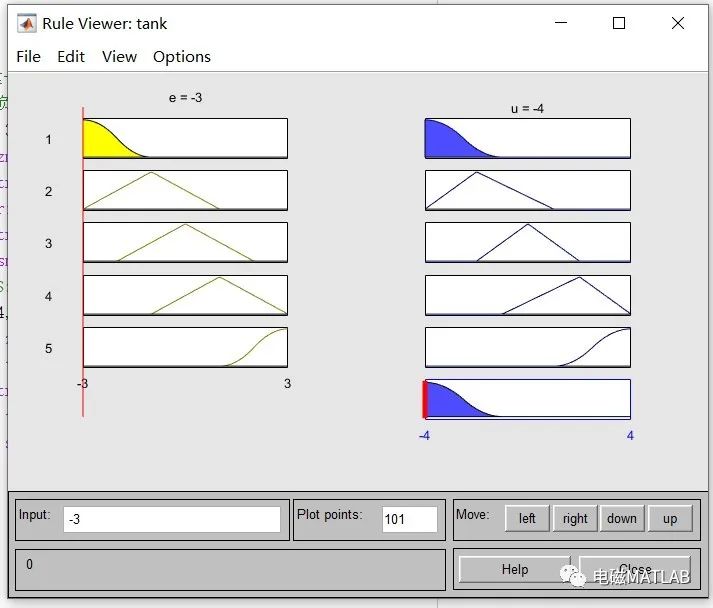
模糊控制响应表见4-4

7 matlab仿真结果

1）模型

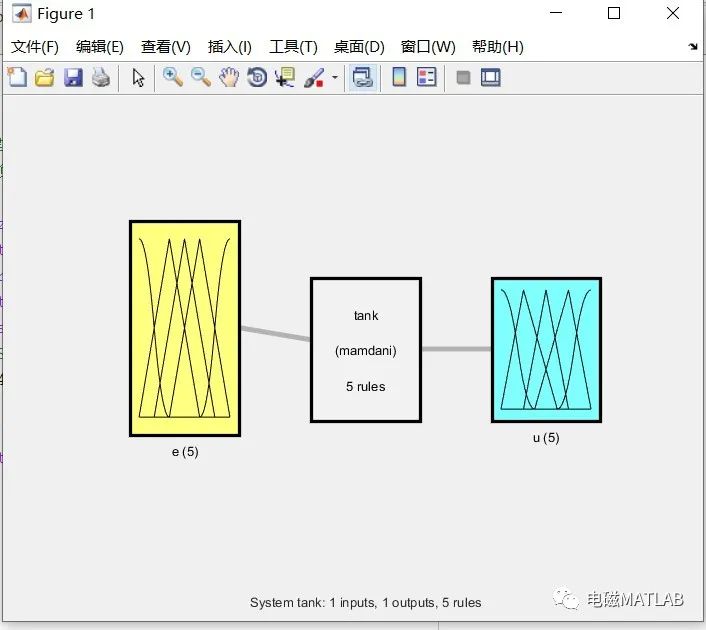
2）输入隶属度

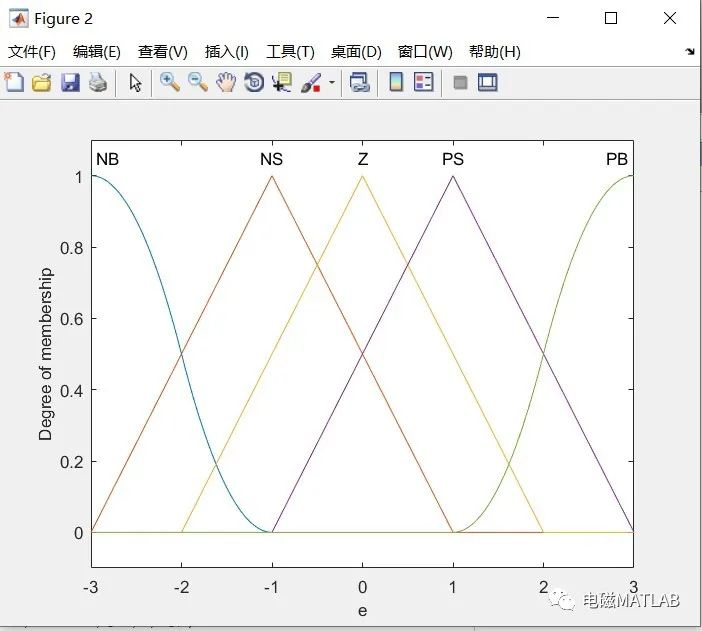
3）输出隶属度

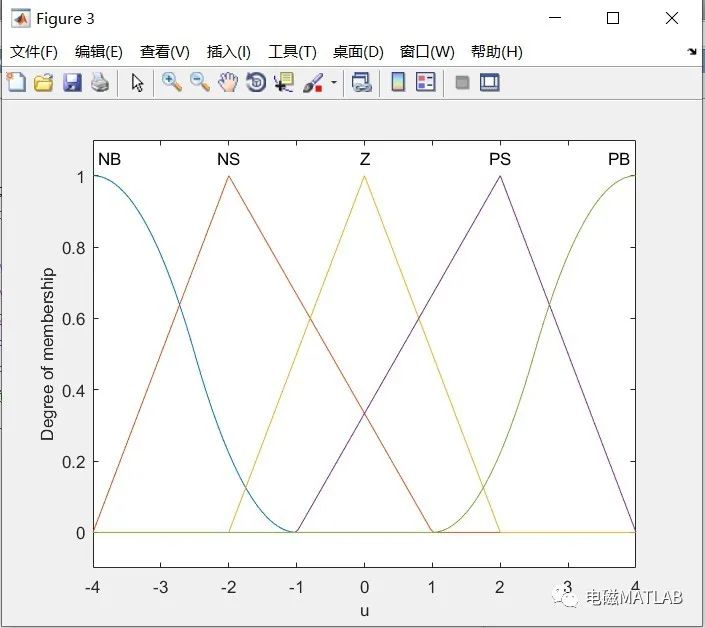
4）控制系统

7 matlab程序

clear clcclose all;a=newfis('fuzz-tank');%创建一个模糊推理系统（FIS）%% 偏差参数%水位变化e划分，NB:负大 NS:负小 Z:零 PS:正小 PB:正大a=addvar(a,'input','e',[-3,3]);%向模糊推理系统中添加语言变量a=addmf(a,'input',1,'NB','zmf',[-3,-1]); %Z形隶属函数a=addmf(a,'input',1,'NS','trimf',[-3,-1,1]);%三角形隶属函数a=addmf(a,'input',1,'Z','trimf',[-2,0,2]);a=addmf(a,'input',1,'PS','trimf',[-1,1,3]);a=addmf(a,'input',1,'PB','smf',[1,3]);%S形隶属函数%% 控制参数%控制量u变化划分，NB:负大 NS:负小 Z:零 PS:正小 PB:正大a=addvar(a,'output','u',[-4,4]);a=addmf(a,'output',1,'NB','zmf',[-4,-1]);a=addmf(a,'output',1,'NS','trimf',[-4,-2,1]);a=addmf(a,'output',1,'Z','trimf',[-2,0,2]);a=addmf(a,'output',1,'PS','trimf',[-1,2,4]);a=addmf(a,'output',1,'PB','smf',[1,4]);%% 规则描述%模糊规则%若e负大，则u负大%若e负小，则u负小%若e为零，则u为零%若e正小，则u正小%若e正大，则u正大rulelist=[    1 1 1 1;    2 2 1 1;    3 3 1 1;    4 4 1 1;    5 5 1 1];a=addrule(a,rulelist);%% %将DefuzzMethod属性设置为moma1=setfis(a,'DefuzzMethod','mom');%将DefuzzMethod属性设置为momwritefis(a1,'tank');%保存文件到磁盘上a2=readfis('tank');%读取模糊控制系统
figure(1);plotfis(a2);%绘制FIS系统结构figure(2);plotmf(a,'input',1);figure(3);plotmf(a,'output',1);
flag=1;if flag==1    showrule(a);    ruleview('tank');enddisp('------------------------------------------------------');disp('     fuzzy controller table:e=[-3, 3],u=[-4, 4]       ');disp('------------------------------------------------------');for i=1:1:7    e(i)=i-4;    Ulist(i)=evalfis([e(i)],a2);endUlist=round(Ulist)%取整e=-3;u=evalfis([e],a2)