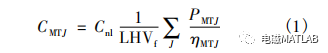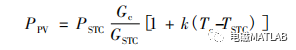改进粒子群优化算法-凡亿课堂

参考文献《改进粒子群优化算法的概率可用输电能力研究-李国庆》

1 粒子群算法

粒子群算法（Particle Swarm Optimization，PSO）是一种基于群体智能的优化算法，是一种基于仿生学的优化算法。粒子群算法是通过模拟鸟群、鱼群等群体行为来实现优化的算法。粒子群算法最初由美国社会学家Kennedy和Eberhart于1995年提出，其基本思想是通过模拟鸟群、鱼群等群体行为来实现优化的算法。粒子群算法的基本思想是将待优化的问题看作是一个多维空间中的搜索问题，将每个解看作是空间中的一个粒子，每个粒子在空间中移动，每个粒子的当前位置和速度都受到个体历史最优位置和全局历史最优位置的影响，从而实现全局最优解的搜索。在粒子群算法中，每个粒子代表一个解，每个粒子的位置和速度都可以描述为一个向量。在每一次迭代中，每个粒子都会根据当前位置和速度更新自己的位置和速度，并计算出当前位置的适应度值。粒子的速度和位置的更新规则是通过不断地迭代来实现的，每一次迭代都会更新粒子的速度和位置，并计算出当前位置的适应度值。适应度值是判断解的好坏的标准，适应度值越小表示解越好，适应度值越大表示解越差。粒子的速度和位置的更新规则是通过不断地迭代来实现的，每一次迭代都会更新粒子的速度和位置，并计算出当前位置的适应度值。适应度值是判断解的好坏的标准，适应度值越小表示解越好，适应度值越大表示解越差。粒子群算法的优点是收敛速度快、易于实现、对初始值不敏感、具有全局搜索能力等。但是，粒子群算法也存在一些缺点，如易陷入局部最优、对参数的选择敏感等。总之，粒子群算法是一种基于群体智能的优化算法，其基本思想是通过模拟鸟群、鱼群等群体行为来实现优化的算法。粒子群算法具有收敛速度快、易于实现、对初始值不敏感、具有全局搜索能力等优点，但是也存在易陷入局部最优、对参数的选择敏感等缺点。在实际应用中，需要根据具体问题的特性来选择是否使用粒子群算法以及如何选择算法的参数。2 改进粒子群算法
惯性权重w对 PSO 算法的优化性能影响很大。研究表明，较大的w值有利于跳出局部最优，而较小的w有利于加速收敛。因此,本文从收敛速度和搜索范围上对 PSO 进行改进，采用动态改变惯性权重的策略，使得

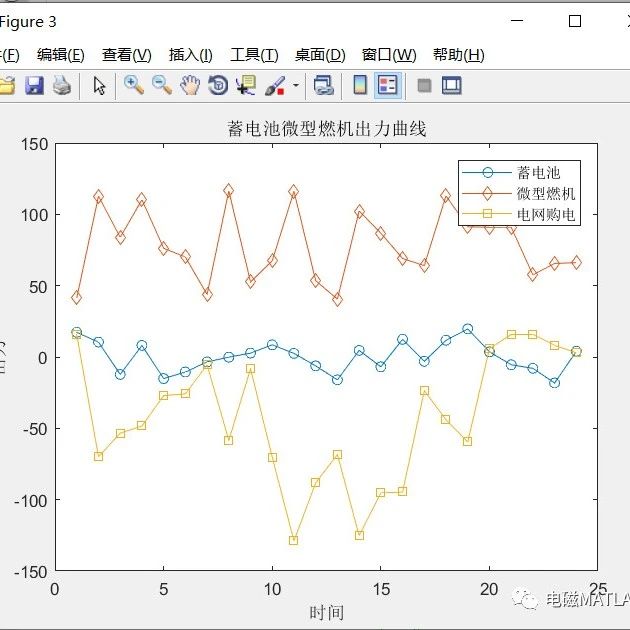
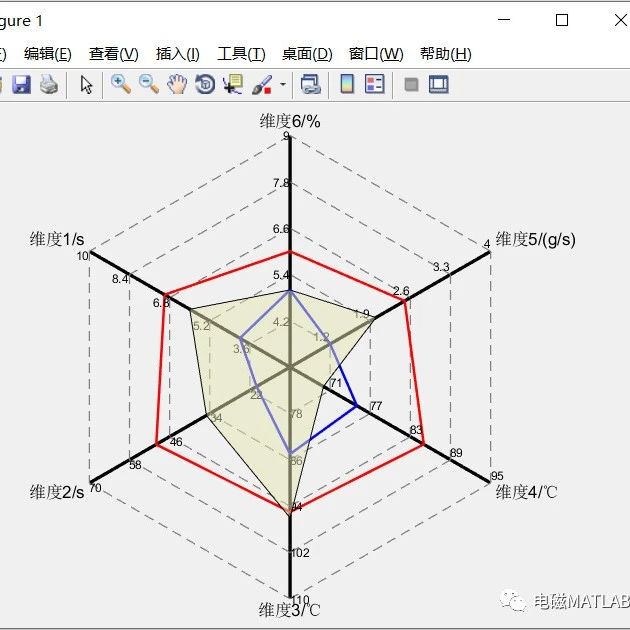
3 算例

4 结果对比

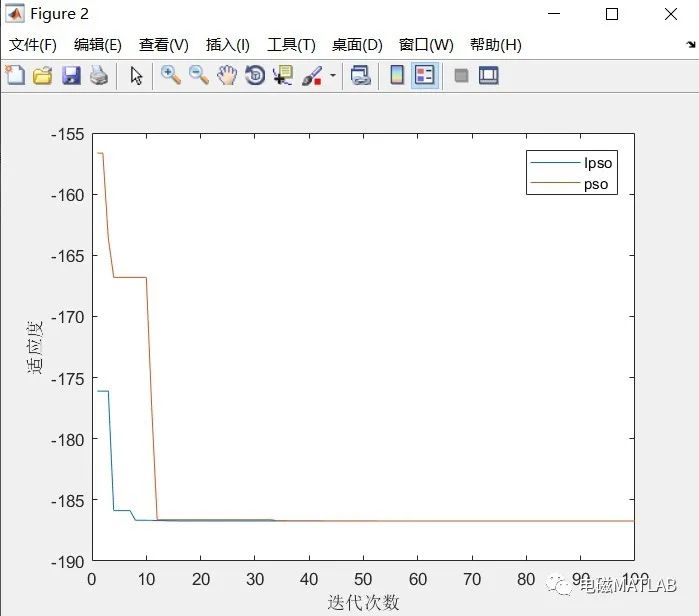
5 matlab程序
1）主函数

% 自适应惯性权重粒子群算法版（改进粒子群）clc;clear;close all;
%% 算法参数nVar=2; %变量个数VarMin=-10*ones(1,2); % 变量下限
VarMax=10*ones(1,2); % 变量上限MaxIt=100; % 最大迭代次数nPop=200; % 种群规模
%% iaPSO Parameters CostFunction=@(x) fun_objective(x); % Cost Functionw=1; % Inertia Weightwdamp=0.99; % Inertia Weight Damping Ratioc1=1.5; % Personal Learning Coefficientc2=2.0; % Global Learning CoefficientVarSize=[1 nVar]; % Size of Decision Variables Matrix% Velocity LimitsVelMax=0.1*(VarMax-VarMin);VelMin=-VelMax;
%% Initialization
empty_particle.Position=[];empty_particle.Cost=[];empty_particle.Velocity=[];empty_particle.Best.Position=[];empty_particle.Best.Cost=[];
particle=repmat(empty_particle,nPop,1);
GlobalBest.Cost=inf;
for i=1:nPop % Initialize Position particle(i).Position=unifrnd(VarMin,VarMax,VarSize); % Initialize Velocity particle(i).Velocity=zeros(VarSize); % Evaluation particle(i).Cost=CostFunction(particle(i).Position); % Update Personal Best particle(i).Best.Position=particle(i).Position; particle(i).Best.Cost=particle(i).Cost; % Update Global Best if particle(i).Best.Cost GlobalBest=particle(i).Best; end end
BestCost=zeros(MaxIt,1);%自适应权重ak=zeros(MaxIt,1);

%% PSO Main Loopfor it=1:MaxIt for i=1:nPop % Update Velocity particle(i).Velocity = w*particle(i).Velocity ... c1*rand(VarSize).*(particle(i).Best.Position-particle(i).Position) ... c2*rand(VarSize).*(GlobalBest.Position-particle(i).Position); % Apply Velocity Limits particle(i).Velocity = max(particle(i).Velocity,VelMin); particle(i).Velocity = min(particle(i).Velocity,VelMax); % Update Position particle(i).Position = particle(i).Position particle(i).Velocity; % Velocity Mirror Effect IsOutside=(particle(i).PositionVarMax); particle(i).Velocity(IsOutside)=-particle(i).Velocity(IsOutside); % Apply Position Limits particle(i).Position = max(particle(i).Position,VarMin); particle(i).Position = min(particle(i).Position,VarMax); % Evaluation particle(i).Cost = CostFunction(particle(i).Position); % Update Personal Best if particle(i).Cost particle(i).Best.Position=particle(i).Position; particle(i).Best.Cost=particle(i).Cost; % Update Global Best if particle(i).Best.Cost GlobalBest=particle(i).Best; end end end BestCost(it)=GlobalBest.Cost; deltak=abs(particle(i).Cost-BestCost(it)); ak(it)=sum(deltak)/nPop ;% disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCost(it))]); if it==1 w=w*wdamp; else w=exp(-ak(it)/ak(it-1)); end plot(BestCost(1:it)); xlabel('迭代次数'); ylabel('适应度'); drawnow end%% 输出bestPosition = GlobalBest.Position;fitValue = GlobalBest.Cost;disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCost(it))]);display(['改进粒子群算法获得的最优变量为 : ', num2str(bestPosition)]);display([' 获得的最优目标函数: ', num2str(fitValue)]);best=BestCost';
%% 传统粒子群[ bestPosition, fitValue,BestCost1 ] = PSOFUN( @fun_objective,nVar,VarMin,VarMax,MaxIt,nPop );best1=BestCost1';%% 迭代曲线对比figure plot(best(1:it)); hold on plot(best1(1:it));xlabel('迭代次数');ylabel('适应度');legend('Ipso','pso')

2）子函数

function fun = fun_objective(x)s1 = 0; s2 = 0; for i = 1:5 s1 = s1 i*cos((i 1)*x(1) i); s2 = s2 i*cos((i 1)*x(2) i); end fun = s1*s2;
end

function [ bestPosition, fitValue ,BestCost] = ...PSOFUN( CostFun,nVar,VarMin,VarMax,MaxIt,nPop )% Copyright (c) 2015, Yarpiz (www.yarpiz.com)% All rights reserved. Please read the "license.txt" for license terms.%% Project Code: YPEA102% Project Title: Implementation of Particle Swarm Optimization in MATLAB% Publisher: Yarpiz (www.yarpiz.com)% % Developer: S. Mostapha Kalami Heris (Member of Yarpiz Team)% % Contact Info: sm.kalami@gmail.com, info@yarpiz.com%%% PSO Parameters CostFunction=@(x) CostFun(x); % Cost Functionw=1; % Inertia Weightwdamp=0.99; % Inertia Weight Damping Ratioc1=1.5; % Personal Learning Coefficientc2=2.0; % Global Learning CoefficientVarSize=[1 nVar]; % Size of Decision Variables Matrix% Velocity LimitsVelMax=0.1*(VarMax-VarMin);VelMin=-VelMax;
%% Initialization
empty_particle.Position=[];empty_particle.Cost=[];empty_particle.Velocity=[];empty_particle.Best.Position=[];empty_particle.Best.Cost=[];
particle=repmat(empty_particle,nPop,1);
GlobalBest.Cost=inf;
for i=1:nPop % Initialize Position particle(i).Position=unifrnd(VarMin,VarMax,VarSize); % Initialize Velocity particle(i).Velocity=zeros(VarSize); % Evaluation particle(i).Cost=CostFunction(particle(i).Position); % Update Personal Best particle(i).Best.Position=particle(i).Position; particle(i).Best.Cost=particle(i).Cost; % Update Global Best if particle(i).Best.Cost GlobalBest=particle(i).Best; end end
BestCost=zeros(MaxIt,1);
%% PSO Main Loop
for it=1:MaxIt for i=1:nPop % Update Velocity particle(i).Velocity = w*particle(i).Velocity ... c1*rand(VarSize).*(particle(i).Best.Position-particle(i).Position) ... c2*rand(VarSize).*(GlobalBest.Position-particle(i).Position); % Apply Velocity Limits particle(i).Velocity = max(particle(i).Velocity,VelMin); particle(i).Velocity = min(particle(i).Velocity,VelMax); % Update Position particle(i).Position = particle(i).Position particle(i).Velocity; % Velocity Mirror Effect IsOutside=(particle(i).PositionVarMax); particle(i).Velocity(IsOutside)=-particle(i).Velocity(IsOutside); % Apply Position Limits particle(i).Position = max(particle(i).Position,VarMin); particle(i).Position = min(particle(i).Position,VarMax); % Evaluation particle(i).Cost = CostFunction(particle(i).Position); % Update Personal Best if particle(i).CostbestPosition = GlobalBest.Position;fitValue = GlobalBest.Cost;disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCost(it))]);

登录后查看更多