今天我们来分析在电源电路中比较常见的,一种提高功率因数的电路——填谷电路(Valley Fill Circuit)。
我们知道,在交流电路中,电压是正弦波形式的。如果负载是一个纯电阻,那么电压和电流的相位是完全一样的,如下图所示:
(图中的RL3是用作电流取样的,下同)
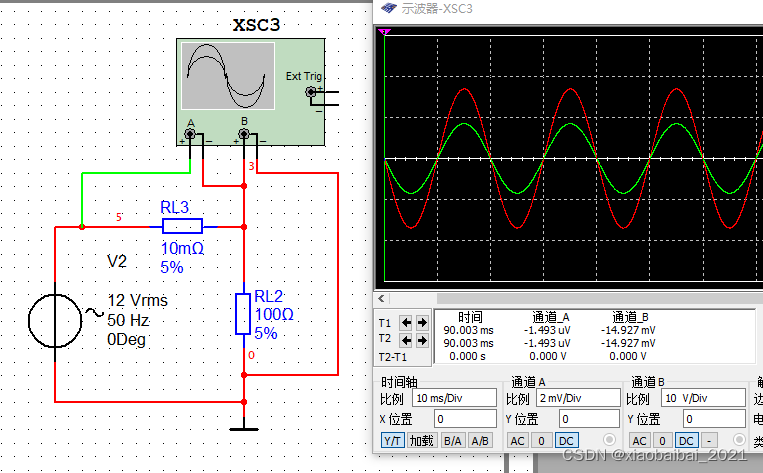
而如果负载是一个电容(或电感),那么电压和电流的相位就不同,如下图所示:
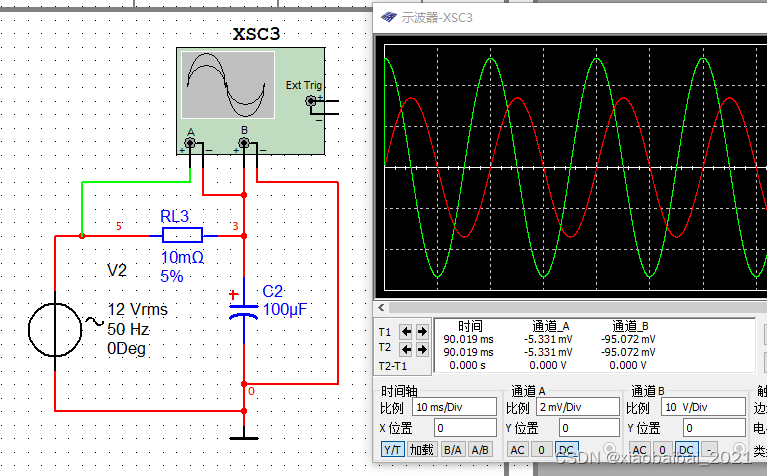
在交流电路中,电压与电流之间的相位差(Φ)的余弦叫做功率因数,用符号cosΦ表示。在数值上,功率因数是有功功率和视在功率的比值:

功率因数是衡量电气设备效率高低的一个系数。功率因数低,说明电路用于交变磁场转换的无功功率大,从而降低了设备的利用率,增加了线路供电损失。
我们可以简单理解一下,如果负载是纯电阻性的,那么电压和电流同相位,功率因数为1,电源提供的功率都消耗在负载上;如果负载是纯电抗性的,那么电压和电流相差90°,功率因数为0,那么有很多功率都消耗在线路上。
电路中只要存在电压和电流相位不同或波形不同,都会使得功率因数小于1。
对于电路中有容性负载(或者感性负载)的电路,提高功率因数的方法是并电感(或者并电容),使得电容和电感性质抵消,但是对于一些电路中有非线性器件(如二极管)的电路,就需要依具体情况来设计了。我们接下来要讲的填谷电路,就是用于提高整流电路的功率因数的。
首先我们来看一下最基本的整流电路。
如图,是一个基本的整流桥电路,交流电输入后,经过整流、输出端经电容滤波后,加到一个负载上。
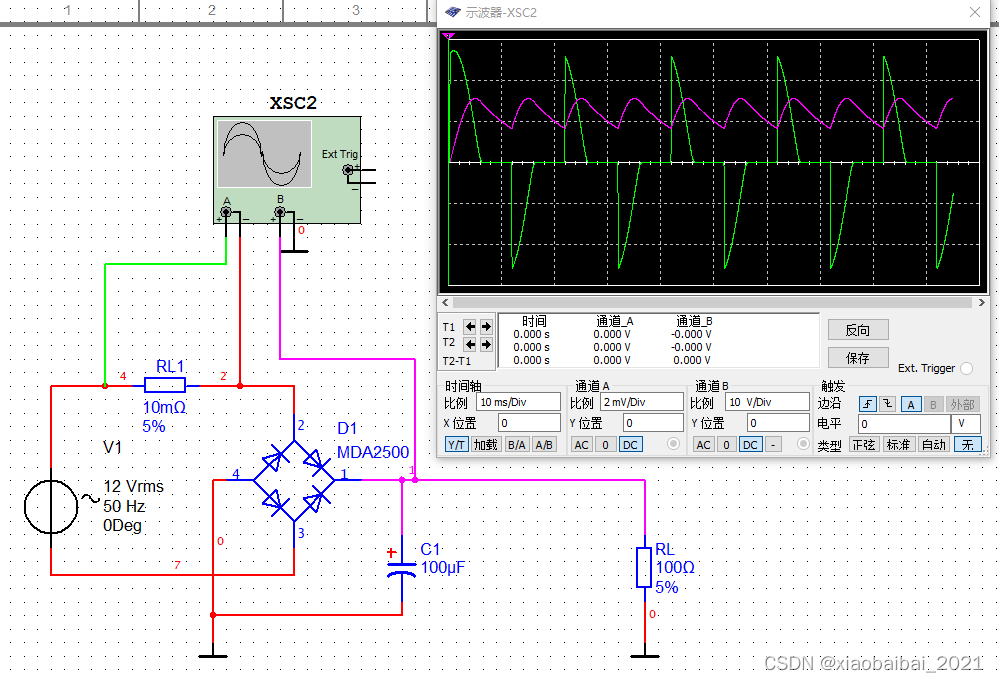
图中示波器显示的绿色线是电流,可以发现,与输入电压(正弦波)波形完全不同,相位也相差较大。
由于电路中存在二极管(非线性器件)、电容,都会使得电压和电流相位不同;一方面,由于电容的充放电,只有输入电压高于电容电压V1时,才会有电流为后端的电容和负载供电;另一方面,电容的存在会使得电流相位超前于电压。因此该电路的功率因数较低。
填谷电路的基本形式如下图,整流后的电压,接到电路的 端和-端:
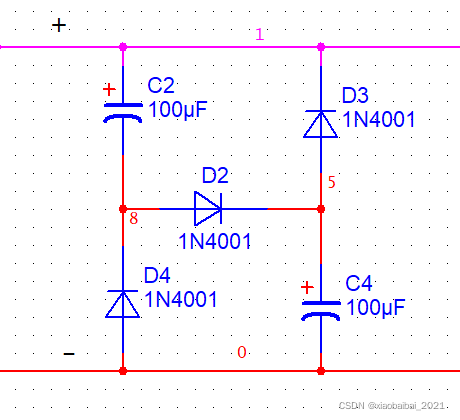
简单分析一下:
在输入电压电压较高时,电流对电容充电,走的是如下路径:
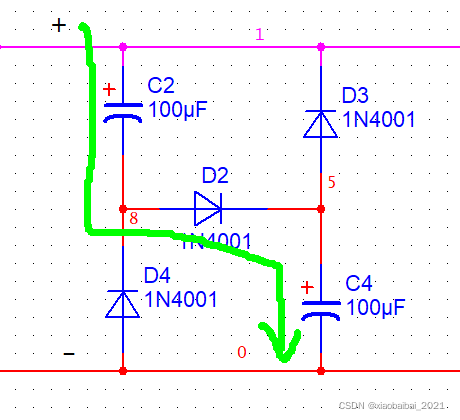
输入电压较低时,电容对外放电,走的是如下路径
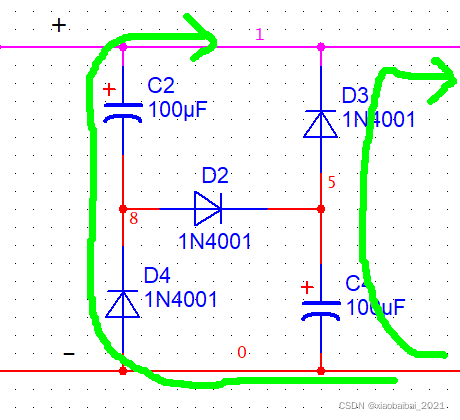
相当于电容是串联充电、并联放电。
假设两个电容电压之和为V1,那么只要整流后的电压高于V1的一半,二极管就会截止,由外部电源为负载供电。
对比基本的整流电路,需要整流后的电源高于V1,才会由外部电源供电。
这样的好处是,增加了一个周期内外部电源的供电时间;同时,也由于导通时间变长,只需要较小的峰值电流就满足一个周期内的功率要求。
填谷电路可以把电流的尖峰填平,因此而得名。
填谷电路的仿真图如下:
可以看出,一个周期内的电流波形,时间更长、峰值更小,相比基本的整流电路,电流更接近于正弦形状,因此可以大大提高功率因数。
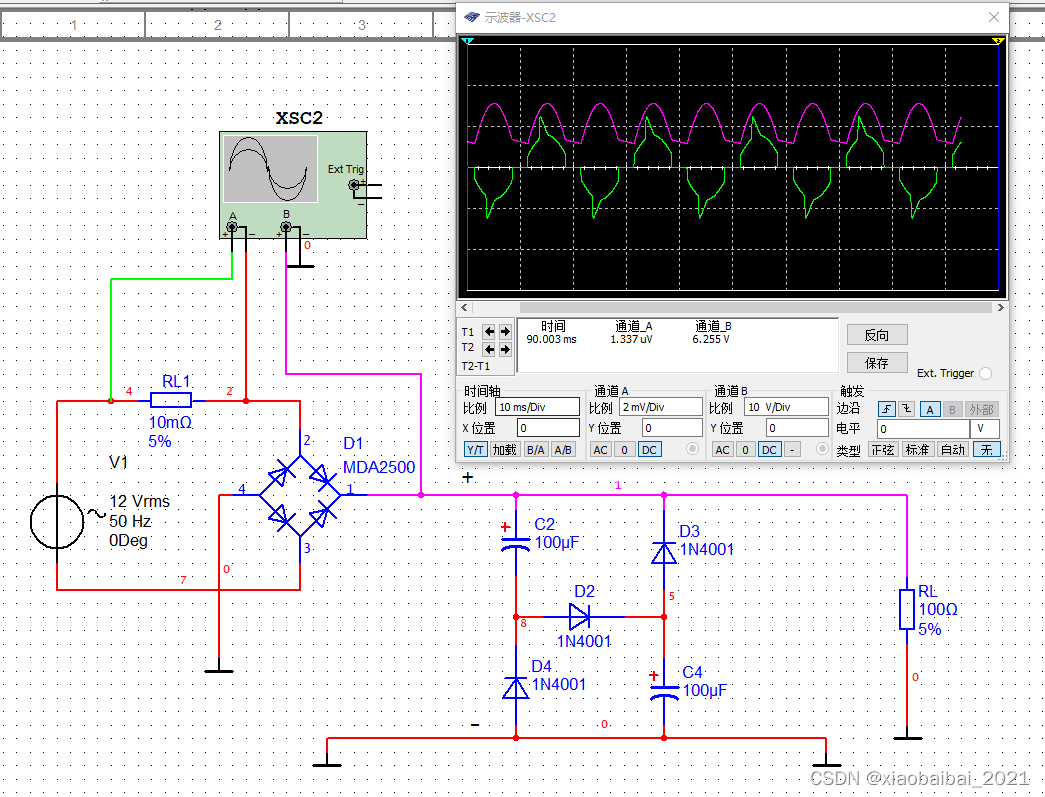
填谷电路一般在节能灯、LED灯、小功率开关电源电路中较常见到。
使用填谷电路时,要注意,两个电容需要特性一致

 扫码关注
扫码关注