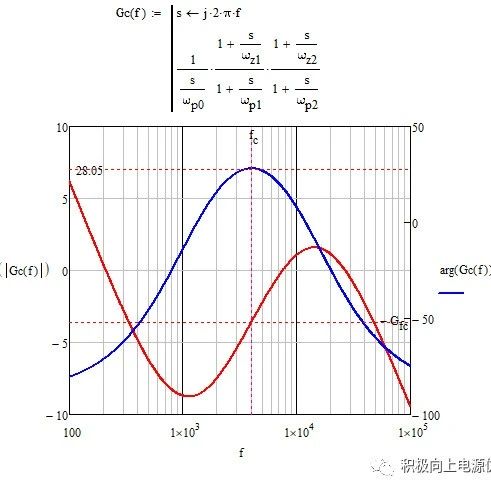
LLC环路设计参考杨波的博士论文《LLC resonant converter》第6章Small signal analysis of LLC resonant converter。
功率级波特图在高于谐振频率时:
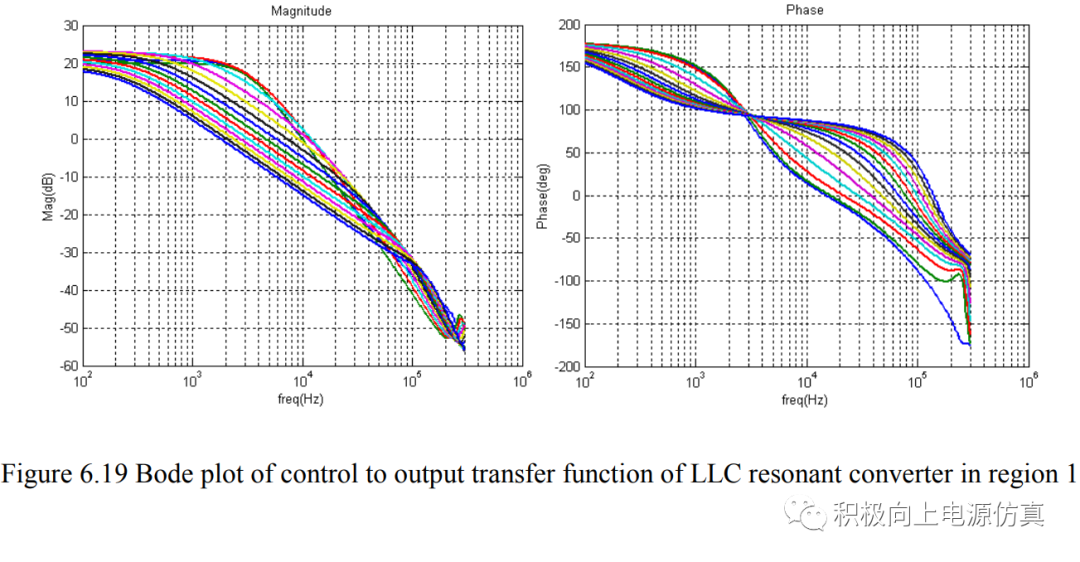
低于谐振频率时:
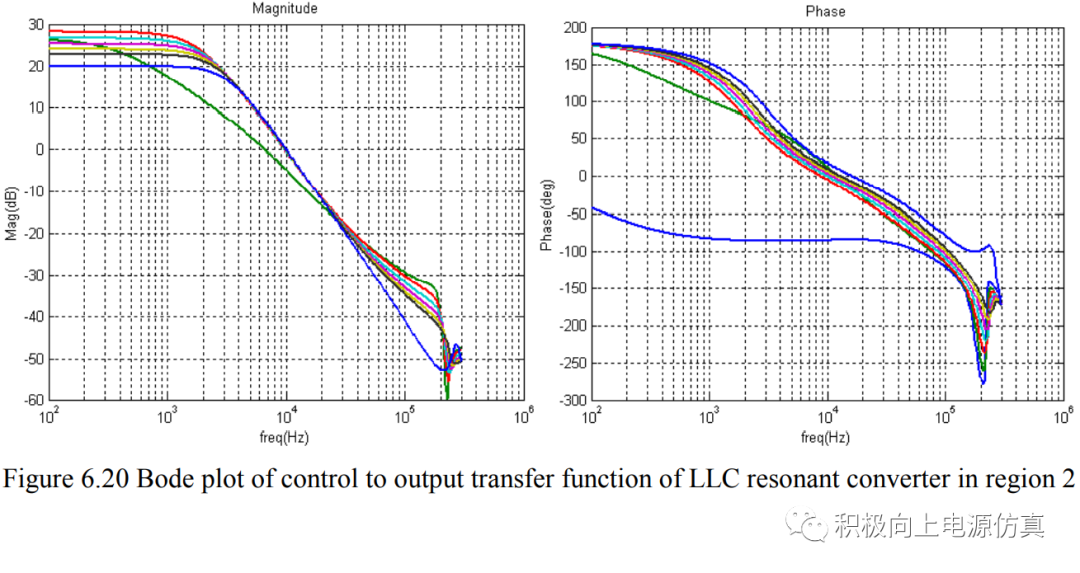
文章指出,LLC低于谐振频率的小信号特性非常稳定,在该区域有两个极点,因为开关频率范围不是很宽,所以双极点不会移动太多。但是该区域有右半平面零点需要避开,带宽通常设计在2~5kHz。
高于谐振频率时极点变化范围较大,轻载时会存在一个低频极点,补偿时需要注意。
在感性区内,增益曲线频率越高增益低,本身为负反馈,补偿器需要设计为正反馈。当频率从感性区跨越到容性区内,相位相差180度。
所以环路补偿设计的工作区域为2区(开关频率低于串联谐振频率)。
在最大增益时用开环扫频得到波特图:
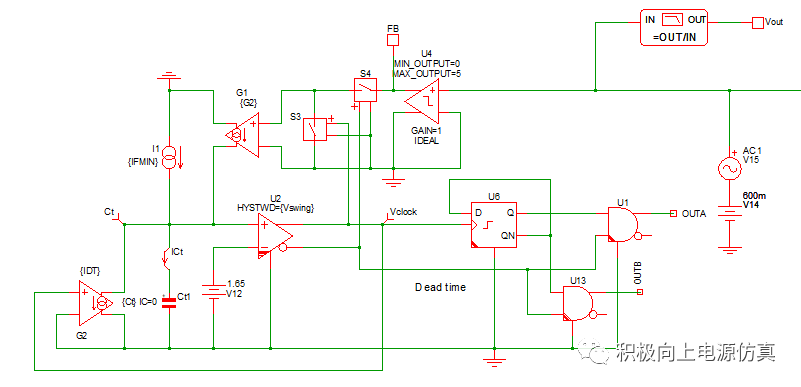

可见功率级初始相位为180度(PWM初始相位为0,补偿器为负反馈):
例如,将穿越频率设置为4k,从功率极波特图中读出该频率下的增益和相位分别为3.59和16.94,然后再通过K因子计算出补偿器参数(从波特图中可看到50k左右有右半平面零点,穿越频率应低于其1/3位置)。
将K因子公式编辑入F11窗口,写入从功率级波特图中获取的期望穿越频率fc处的Gfc,PS,再根据期望的相位裕度PM,即可求出各参数。如下:

将仿真从开环改为闭环,并进行AC分析。

为了避免逻辑混乱,这里使用的NCP1397VCO方案,后续再介绍其工作原理。若用L6599VCO,其相位相差180度。
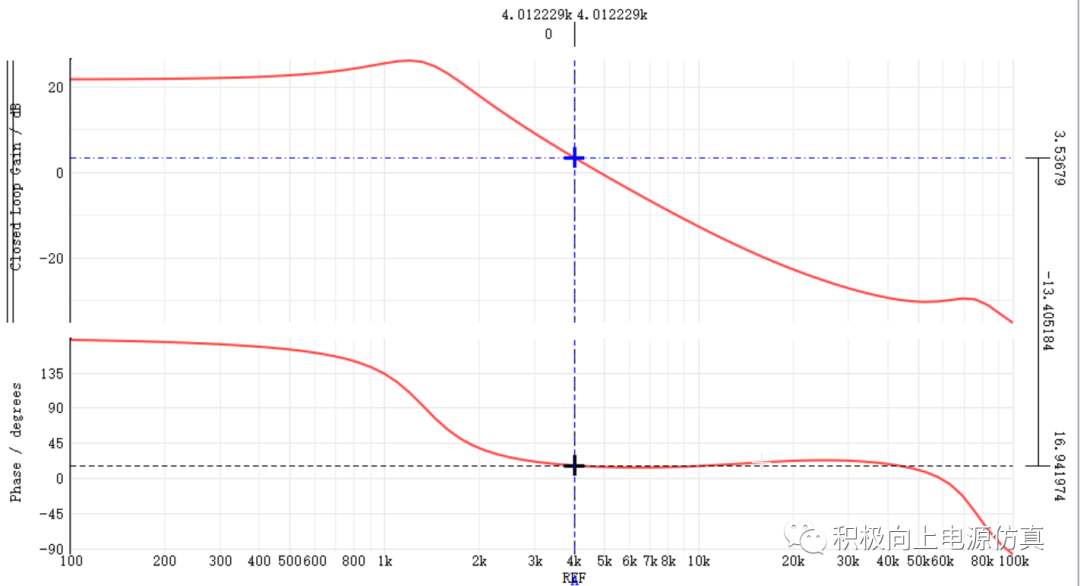
得到波特图:

从波特图可见穿越频率与相位裕量完全符合设计预期。
从仿真器可以查看各参数计算结果:
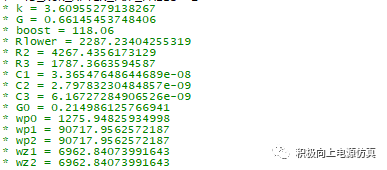
两分钟搞定仿真环路设计,而且非常方便移植。
补偿器波特图:
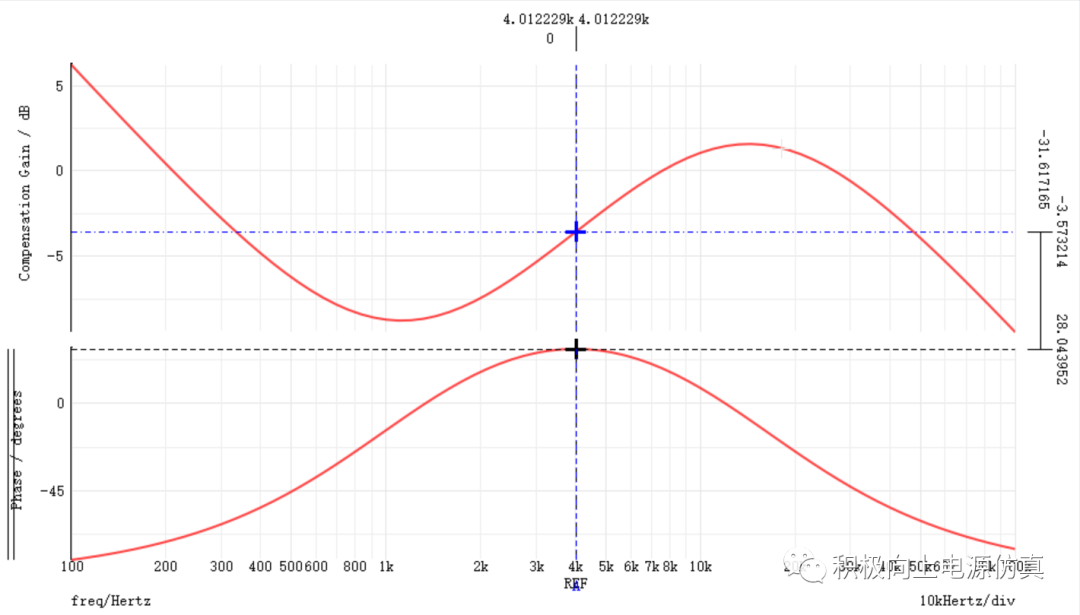
因为使用的K因子法,在fc处刚好是相位提升的最高点。
下面逐一分析k因子的使用及传递函数与k因子公式推导。
1、LLC补偿器相位提升要如何计算
因为功率极在4k时相位为16.94°,而论文说了LLC本身为负反馈(初始相位为180°),其补偿器为正反馈(初始相位为-90°)。而相位裕度为穿越频率处与0度的差值,如果要求相位裕度为45°,那么加起来就是:
-16.94° 180°-90° 45°=118.06°
PM(期望相位裕度)、PS(穿越频率处功率级相位)。boost(需提升相位)。即
boost=PM-PS 90°
很多资料K因子都是boost=PM-PS-90°,为什么会出现这样的差异,就是因为LLC补偿器使用的正反馈,本身少了负号(arg(-1)=180°),导致初始相位差了180度。
2、如何选择补偿器类型并推导传递函数
提升相位超过90度需要使用3P2Z即三型补偿。三型补偿有隔离型和非隔离型,这里使用最简单的OPA非隔离型。
如下图:

传递函数推导即在s域对运放负反馈化简:

标准形式即为:

因为该结果为负反馈,所以需要在仿真上增加了相位取反(U4),即抵消负号。
3、什么是K因子
K因子的穿越频率分布在零点和极点的几何平均值处(两个零点相等,两个极点也相等),即

为什么呢?因为这样放置的零极点使得相位提升在fc处最大,如下图:

图片来源:《开关电源控制环路设计》——BASSO
4、k值与boost关系推导
传递函数在fc处有:
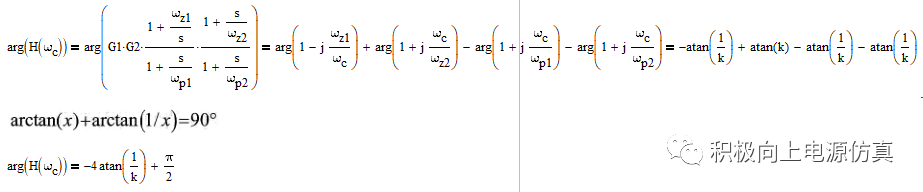
还要补上正反馈的初始相位滞后的90度,得:

很多资料上有平方根号,其实是一样的。
其他类型补偿器k因子也是这样推导的,手动放置零极点也需要这样推导。
5、各电阻电容如何求解
已知R1,fc,fp12,fz12,G,所以在fc穿越频率处的增益为:

G为在fc处需要提升的增益。
由此可求得R2:
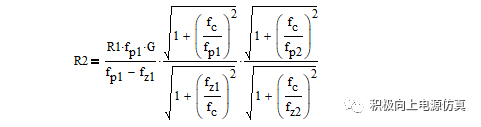
求得R2后可依次求得:
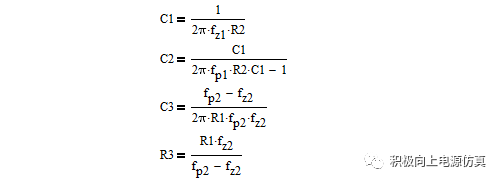
6、公式推导完成,代入参数计算



可见计算结果与仿真器计算一致。
三型补偿K因子公式:
****Voltage loop***********
.VAR fc = 4k
.VAR Gfc = 3.59
.VAR PS = 16.94
.VAR PM = 45
.VAR boost = PM-PS 90
.VAR G = 10^(-Gfc/20)
.VAR k = tan((boost/4 45)*(pi/180))
.VAR fz1 = fc/k
.VAR fz2 = fc/k
.VAR fp1 = k*fc
.VAR fp2 = k*fc
.VAR C2 = 1/(2*pi*fc*G*R1)
.VAR C1 = C2*(k^2-1)
.VAR R2 = K/(2*pi*fc*C1)
.VAR R3 = R1/(k^2-1)
.VAR C3 = 1/(2*pi*fc*k*R3)
.VAR wp0 = 1/(R1*(C1 C2))
.VAR wp1 = 1/(R2*((C1*C2)/(C1 C2)))
.VAR wp2 = 1/(R3*C3)
.VAR wz1 = 1/(R2*C1)
.VAR wz2 = 1/((R1 R3)*C3)
.VAR G0 = R2/(R1*C1/(C1 C2))
.VAR fp0 = wp0/(2*pi)
.VAR fp1 = wp1/(2*pi)
.VAR fp2 = wp2/(2*pi)
.VAR fz1 = wz1/(2*pi)
.VAR fz2 = wz2/(2*pi)
将以上公式代入simplis即可实现快速仿真,只需要更改前4行。
实际情况中K因子法有很多局限性,比如隔离型环路中K因子求得的极点与光耦的极点不一定能重合,这时候就需要手动放置,然后再计算其他零极点位置,后续分享。

 扫码关注
扫码关注