上期我们谈到电路分析中的叠加定理定理,事实上很多小白最常接触的虽然是叠加定理,但在特殊场合用等效电源定理更多,所以了解等效电源定理是很有必要的。
1、二端网络
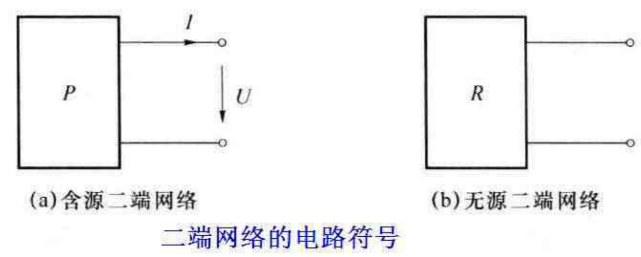
等效电源定理应用的对象是二端网络,具有两个输出端与外电路相连接,不论其内部结构如何,均称为二端网络,或称为-端口网络。二端网络的内部结构可以是元件数较少的简单电路,也可以是含有多个电阻与电源的复杂电路,最简单的二端网络中只包含一个电阻元件。不管二端网络的内部结构如何,二端网络--定有两个接线端与外电路相连,并且在网络端口处流入的电流一定等于流出的电流。
按照二端网络内部是否连接有电源,可以将二端网络分为含源二端网络与无源二端网络。下图所示为二端网络的电路符号:
2、等效电源定理
在有些情况下,人们只需要计算复杂电路中某一元件或某一支路的电压、电流和功率时,可以将余下的含有电源的部分电路用-个等效电源来代替。由于余下的部分电路与某一支路或某一元件必须有两个出线端相连接,因此称为有源线性二i端网络。有源二端网络可以是简单电路,也可以是复杂电路。但从某一支路或某一元件来看,余下的有源线性二端网络可以化简成一个等效电源,这种化简成一个等效电源的方法,称为等效电源定理,如下图所示:
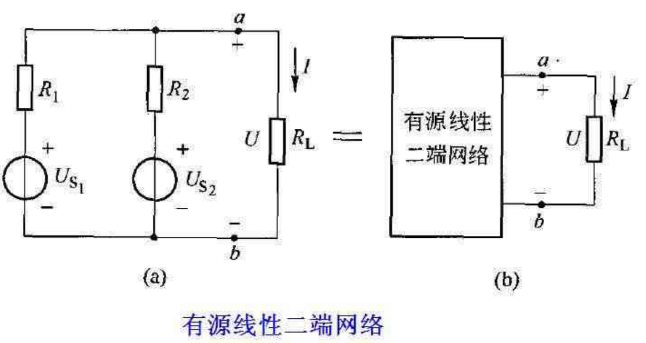
在上图中,计算R L中的电流、端电压和功率时,把a、b左侧的含源电路化简为-一个有源二端网络,如图中的(b)所示。对R来说是等效的。因为有源线性.端网络向RL供电时,仍然保持R.中的电流,端电压和功率不变。
由于电源可以用两种等效电路表示,故有源线性二端网络可以等效成一个电压源,也可以等效成一个电流源,因此有两个等效电源定理。等效成电压源的,称为戴维南定理,等效成电流源的称为诺顿定理。
3、戴维南定理
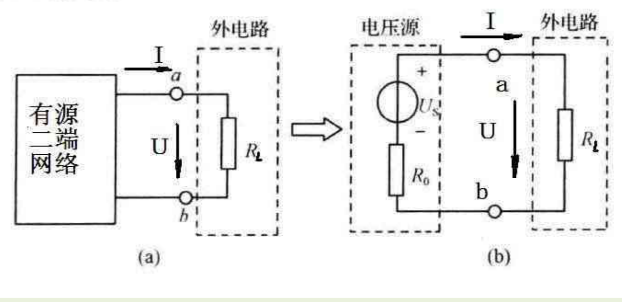
戴维南定理的内容:任何一个复杂的线性有源二端网络,就其对外电路的作用来说,都可以用一个等效的电压源来代替,等效电压源的电动势E就等于有源二端网络的开路电压U。。其内阻R。等于该有源二端网络除源后,所得的无源网络两端间的等效电阻。
可见,应用戴维南定理简化电路,关键是求有源二端网络的开路电压和除源后的网络等效电阻。所谓除源,就是将原有源二端网络内所有的理想电压源短接,令其电动势为零;理想电流源开路,令其电流Is为零。
在电路分析中,若只需计算某一-支路的电流和电压,应用戴维南定理就十分方便,只要将这一支路移去,使电路断开,留下的部分即为一个有源二端网络,然后按照戴维南定理求出等效电压源的Us和R。如下图所示。
4、诺顿定理
戴维南定理告诉我们,有源二端网络可用电压源来等效代替,故戴维南定理又称为等效电压源定理。由于电压源与电流源可以等效变换,因此有源二端网络也可用电流源来等效代替,这就是诺顿定理,可表述如下:
诺顿定理:任一线性有源二端网络,对其外部电路来说,可用个电流为Is的理想电流源和内阳R。相并联的有源电路来等效代替。
其中,理想电流源的电流Is等于网络的短路电流,内阻R等于相应的无源二端网络的等效电阻。戴维南定理与诺顿定理的关系如下图所示:
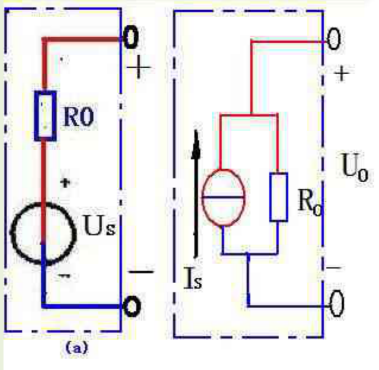
诺顿定理也叫作等效电源流定理,它和戴维南定理仪器合称为等效电源定理。

 扫码关注
扫码关注



































![电子设计:工程中的带通采样定理 [学以致用系列课程之数字信号处理]](https://api.fanyedu.com/uploads/image/8d/7cf32c2b7d6d9e85bef18595362eea.png)


































