扫码关注
随着时代高速度发展，数字电路系统已经历过多种阶段，在此发展过程中，诞生了逻辑代数的三条规则，分别是代入规则、反演规则和对偶规则，但有很多人不太熟悉，所以本文将详谈逻辑代数运算的三条规则。
1、代入规则
在任何一个逻辑等式中，如果以某个逻辑变量或逻辑函数同时取代等式两端的任何一个逻辑变量，则等式依然成立，这个规则称为代入规则。
举例：已知等式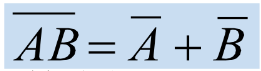
，用函数Y=AC替代等式中的A，根据代入规则，等式依然成立，如图所示：
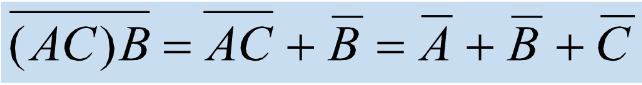
2、反演规则
如果将逻辑函数Y中的“.”变为“+”，“+”变为“.”；“0”变为“1”，“1”变为“0”；原变量变为反变量，反变量变为原变量，那么新得到的逻辑函数表达式就是函数Y的反函数，这一规则称为反演规则。利用反演规则可以方便地求出一个函数的反函数。
使用反演规则时，应注意以下要求：
①要保持原函数中的逻辑运算优先顺序，即要先括号，接着与，然后或，最后非。
②不属于单个变量上的非号要保留不变。
③口诀是“长非、短非互换，与、或互换”
3、对偶规则
若将逻辑函数Y中的“.”变为“+”，“+”变为“.”；“0”变为“1”，“1”变为“0”；而变量保持不变，那么得到的新逻辑函数表达式称为函数Y的对偶式，用Y'表示，也可以说Y和Y'互为对偶式。
对偶规则的内容是：如果两个函数表达式相等，那么它们的对偶式也一定相等。
对偶规则的意义在于：如果两个函数相等，那么它们的对偶函数也一定相等。利用对偶规则，可以使要证明及要记忆的公示数目减少一半。
