本来这期应该讲Buck的尖峰的,不过遇到些问题,所以就往后拖一拖吧,这次来个简单点儿的。
来看看传递函数,也就是我们经常看到的H(s)。
传递函数是怎么定义的呢?
百科是这么定义的:
【传递函数是指零初始条件下线性系统响应(即输出)量的拉普拉斯变换(或z变换)与激励(即输入)量的拉普拉斯变换之比。记作G(s)=Y(s)/U(s),其中Y(s)、U(s)分别为输出量和输入量的拉普拉斯变换】
通俗理解就是,在电路应用中,如果我们把一个电路看作黑匣子,它有输入端,有输出端,传递函数就是输出与输入的比值。

只不过这个比值通常是频率的函数,同时还包含相位信息。s=jw,w就是频率,j包含了相位信息。
传递函数常会在分析环路稳定性,以及滤波器设计中用到,列出了传递函数,剩下的内容其实就是数学的分析了,也就是计算机干的事儿了。
我以前讲过LC滤波器的,使用Matlab画过增益Av曲线,其实也就是传递函数。只不过当时没指出来,道理是一样的。
如何写出传递函数?

这是一个简单的电路,它的传递函数是怎么样的呢?
很简单,运用欧姆定律。如果电路中只有电阻,我们应该都会使用欧姆定律求得输出的电压值。
但是这个电路中还有电感和电容,怎么办呢?
其实我们也可以通过欧姆定律来求得电压值,电感的阻抗是jwL,电容的阻抗是1/jwC,电阻的阻抗是R。输出为电容C上面获得的分压,所以输出与输入的比值为:
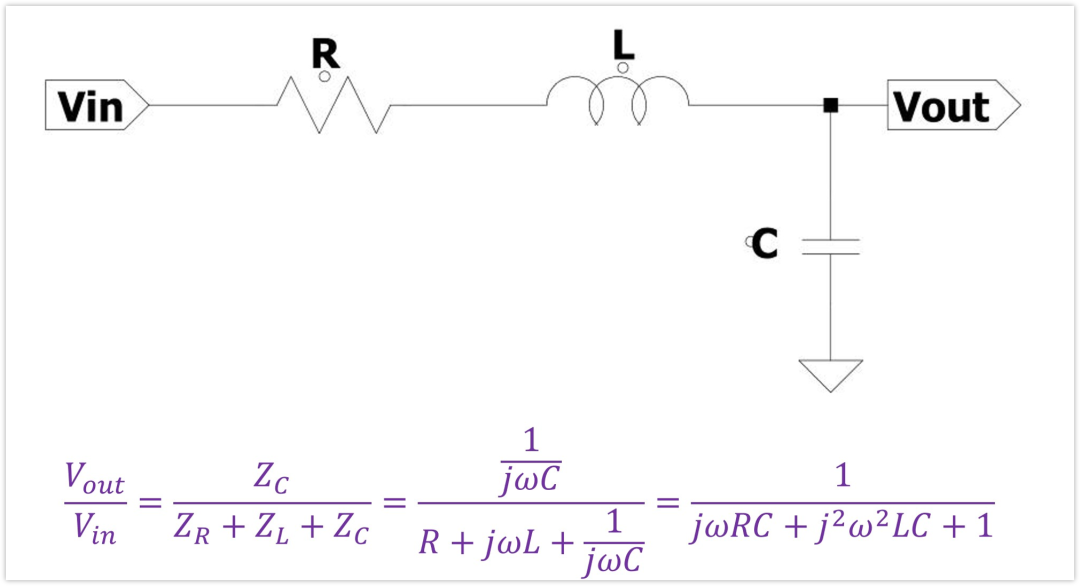
现在我们只需要将自变量改改,令s=jw,传递函数H(s)就出来了。
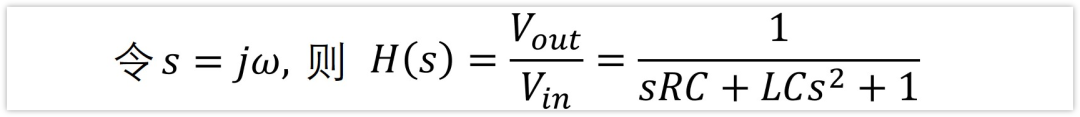
为啥要令s=jw呢?其实这一步就是将傅里叶变换变成了拉普拉斯变换。
啥?我没看到傅里叶变换啊?我感觉我多嘴了。。。
更简单的方式:
我们直接令s=jw,那么电感的阻抗是sL,电容的阻抗1/sC。这样传递函数就能更快出来:
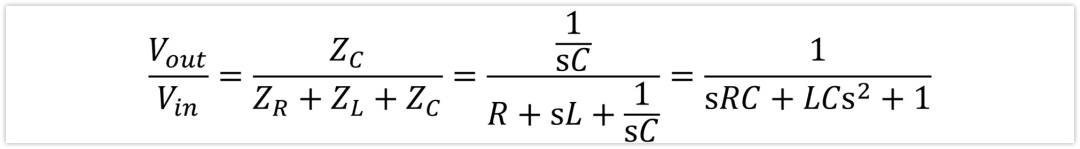
有了传递函数,借助计算机,代入公式,可以很轻松得到幅频曲线和相位曲线。
下图是R=1K,L=1uH,C=1uF时的曲线:
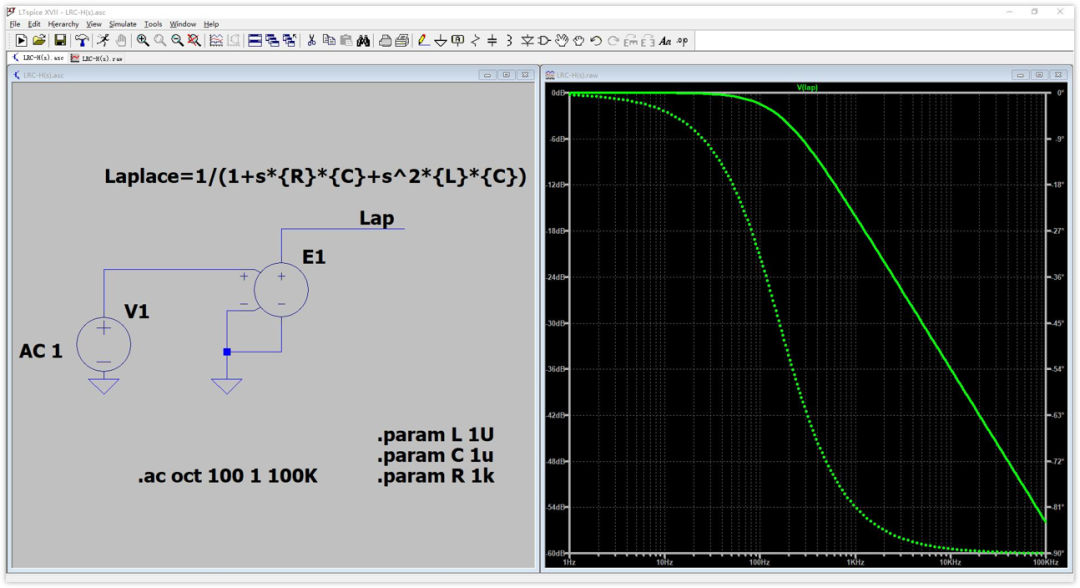
相信现在你应该知道了传递函数到底用来干什么的了吧。
学习资料
有了这个基础,下面给大家推荐个资料,ADI智库的《滤波器设计教程》。
里面有各种滤波器设计电路,以及对应的滤波器的传递函数。所以我们在看文档之前,是要对传递函数有一个基本的了

 扫码关注
扫码关注